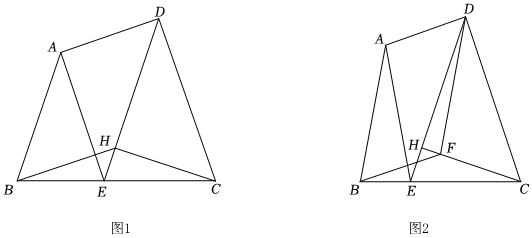
如圖1，四邊形ABCD中，AD⊥CD，邊BC上的點(diǎn)E滿足AB=AE且DC=DE，CH為△CDE的一條高線．
（1）若AE∥CD，求證：
①AD=CH，
②BH⊥AE；
（2）如圖2，點(diǎn)F在線段CH上且BF=CF，求證：四邊形ABFD為平行四邊形．
【考點(diǎn)】四邊形綜合題．
【答案】證明：（1）①證明過程詳見解答；
②證明過程詳見解答；
（2）證明過程詳見解答；
②證明過程詳見解答；
（2）證明過程詳見解答；
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：69引用：1難度：0.1
相似題
-
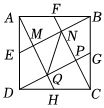1．如圖，點(diǎn)E，F(xiàn)，G，H分別是正方形ABCD的邊DA，AB，BC，CD的中點(diǎn)，連接AH，BE，CF，DG，它們分別相交于點(diǎn)M，N，P，Q，連接NQ．若AB=4，則下列結(jié)論錯誤的是（ ）發(fā)布：2025/5/24 4:0:7組卷：148引用：1難度：0.2 -
2．如圖，矩形AOBC的頂點(diǎn)B，A分別在x軸，y軸上，點(diǎn)C坐標(biāo)是（5，4），D為BC邊上一點(diǎn)，將矩形沿AD折疊，點(diǎn)C落在x軸上的點(diǎn)E處，AD的延長線與x軸相交于點(diǎn)F．
（1）如圖1，求點(diǎn)D的坐標(biāo)；
（2）如圖2，若P是AF上一動點(diǎn)，PM⊥AC交AC于M，PN⊥CF交CF于N，設(shè)AP=t,FN=s,求s與t之間的函數(shù)關(guān)系式；
（3）在（2）的條件下，是否存在點(diǎn)P，使△PMN為等腰三角形？若存在，請直接寫出點(diǎn)P的坐標(biāo)；若不存在，請說明理由．
發(fā)布：2025/5/24 5:0:1組卷：1724引用：8難度：0.1 -
3．定義：有一組對邊相等且這一組對邊所在直線互相垂直的凸四邊形叫做“等垂四邊形”，如圖1，四邊形ABCD中，AB=CD、AB⊥CD，四邊形ABCD即為等垂四邊形，其中相等的邊AB，CD稱為腰，另兩邊AD，BC稱為底
【提出問題】
（1）如圖2，△ABC與△DEC都是等腰直角三角形．∠ACB=∠DCE=90°，135°＜∠AEC＜180°．求證：四邊形BDEA是“等垂四邊形”；
【拓展探究】
（2）如圖3，四邊形ABCD是“等垂四邊形”，AD≠BC，點(diǎn)M、N分別是AD，BC的中點(diǎn)，連接MN．已知腰AB=5，求MN的長；
【綜合運(yùn)用】
（3）如圖4，四邊形ABCD是“等垂四邊形”，AB=CD=4，底BC=9，則較短的底AD長的取值范圍為 ．
發(fā)布：2025/5/24 5:0:1組卷：466引用：1難度：0.1
相關(guān)試卷