如圖，在平面直角坐標系中，AB∥CD∥x軸，BC∥DE∥y軸，且AB=CD=3cm,OA=5cm,DE=2cm,動點P從點A出發，以每秒1cm的速度，沿ABC路線向點C運動；動點Q從點O出發，以每秒2cm的速度，沿OED路線向點D運動．若P，Q兩點同時出發，其中一點到達終點時，運動停止．
（1）直接寫出B，C，D三個點的坐標；
（2）當P，Q兩點出發2s時，求△OPQ的面積；
（3）設兩點運動的時間為t s,用含t的式子表示運動過程中△OPQ的面積；
（4）在點P，Q運動過程中，點C被包含在△OPQ區域（包含邊界）的時長是 178178s.
17
8
17
8
【考點】三角形綜合題．
【答案】
17
8
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：58引用：1難度：0.1
相似題
-
1．（1）閱讀理解：
如圖1，在△ABC中，若AB=10，AC=6，求BC邊上的中線AD的取值范圍．解決此問題可以用如下方法：延長AD到點E使DE=AD，連接BE（或將△ACD繞著點D逆時針旋轉180°得到△EBD），把AB，AC，2AD集中在△ABE中．利用三角形三邊的關系即可判斷中線AD的取值范圍是；
（2）問題解決：如圖2，在△ABC中，D是BC邊上的中點，DE⊥DF于點D，DE交AB于點E，DF交AC于點F，連接EF，求證：BE+CF＞EF．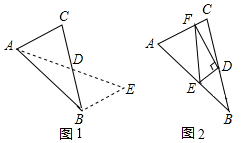
發布：2025/6/17 11:0:1組卷：624引用：7難度：0.4 -
2．把一副三角板按如圖1擺放（點C與點E重合），點B，C（E），F在同一直線上．∠ACB=∠DFE=90°，∠A=30°，∠DEF=45°，BC=EF=8cm,點P是線段AB的中點．△DEF從圖1的位置出發，以4cm/s的速度沿CB方向勻速運動，如圖2，DE與AC相交于點Q，連接PQ．當點D運動到AC邊上時，△DEF停止運動．設運動時間為t（s）．
（1）當t=1時，求AQ的長；
（2）當t為何值時，點A在線段PQ的垂直平分線上？
（3）當t為何值時，△APQ是直角三角形？
發布：2025/6/17 21:30:1組卷：286引用：3難度：0.1 -
3．已知，如圖，在平面直角坐標系中，A為y軸正半軸上一點，B為x軸負半軸上一點．
（1）若BP平分∠ABO，AP平分∠BAO的外角，求∠P．
（2）如圖2，C為x軸正半軸上一點，BP平分∠ABC，且P在AC的垂直平分線上．若∠ABC=2∠ACB，求證：AP∥BC．
（3）在第（2）問的條件下，D是AB上一點，E是x軸正半軸上一點，連AE交DP于H．當∠DHE與∠ABE滿足什么條件時，DP=AE，請說明理由．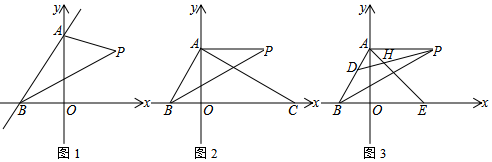
發布：2025/6/17 19:30:1組卷：75引用：1難度：0.3