在學(xué)習(xí)全等三角形知識(shí)時(shí)、數(shù)學(xué)興趣小組發(fā)現(xiàn)這樣一個(gè)模型：它是由兩個(gè)共頂點(diǎn)且頂角相等的等腰三角形構(gòu)成．在相對(duì)位置變化的同時(shí)，始終存在一對(duì)全等三角形．通過(guò)資料查詢，他們得知這種模型稱為“手拉手模型”，興趣小組進(jìn)行了如下操作：
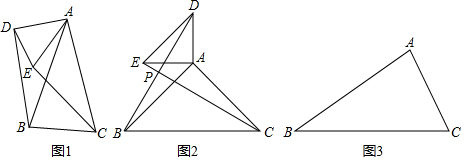
（1）如圖1、兩個(gè)等腰三角形△ABC和△ADE中，AB=AC，AE=AD，∠BAC=∠DAE，連接BD、CE、如果把小等腰三角形的腰長(zhǎng)看作小手，大等腰三角形的腰長(zhǎng)看作大手，兩個(gè)等腰三角形有公共頂點(diǎn)，類似大手拉著小手，這個(gè)就是“手拉手模型”，在這個(gè)模型中，和△ADB全等的三角形是 △AEC△AEC，此時(shí)BD和CE的數(shù)量關(guān)系是 BD=CEBD=CE；
（2）如圖2、兩個(gè)等腰直角三角形ABC和△ADE中，AB=AC，AE=AD，∠BAC=∠DAE=90°，連接BD，CE，兩線交于點(diǎn)P，請(qǐng)判斷線段BD和CE的數(shù)量關(guān)系和位置關(guān)系，并說(shuō)明理由；
（3）如圖3，已知△ABC，請(qǐng)完成作圖：以AB、AC為邊分別向△ABC外作等邊△ABD和等邊△ACE（等邊三角形三條邊相等，三個(gè)角都等于60°），連接BE，CD，兩線交于點(diǎn)P，并直接寫出線段BE和CD的數(shù)量關(guān)系及∠PBC+∠PCB的度數(shù)．
【考點(diǎn)】三角形綜合題．
【答案】△AEC；BD=CE
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：3336引用：15難度：0.3
相似題
-
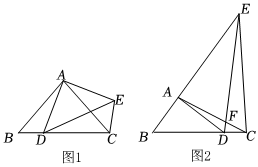1．如圖，Rt△ABC與Rt△ADE的直角頂點(diǎn)重合于點(diǎn)A，點(diǎn)D在BC邊上（不與B，C重合）．
（1）如圖1，當(dāng)∠ABC=∠ADE=45°時(shí)，請(qǐng)直接寫出線段BD，CE之間的數(shù)量關(guān)系．
（2）如圖2，當(dāng)∠ABC=∠ADE=60°時(shí)，設(shè)AC與DE交于點(diǎn)F．①求證EC=BD．②若BD=3，DC=1，試分別探求tan∠FDC和3的值．FDFC發(fā)布：2025/5/24 21:30:1組卷：21引用：1難度：0.2 -
2．（1）感知：如圖①．AB=AD，AB⊥AD，BF⊥AF于點(diǎn)F，DG⊥AF于點(diǎn)G．求證：△ADG≌△BAF；
（2）拓展：如圖②，點(diǎn)B，C在∠MAN的邊AM，AN上，點(diǎn)E，F(xiàn)在∠MAN在內(nèi)部的射線AD上，∠1，∠2分別是△ABE，△CAF的外角，已知AB=AC，∠1=∠2=∠BAC．求證：△ABE≌△CAF；
（3）應(yīng)用：如圖③，在△ABC中，AB=AC，AB＞BC，點(diǎn)在D邊BC上，CD=2BD，點(diǎn)E，F(xiàn)在線段AD上，∠1=∠2=∠BAC．若△ABC的面積為12，則△ABE與△CDF的面積之和為．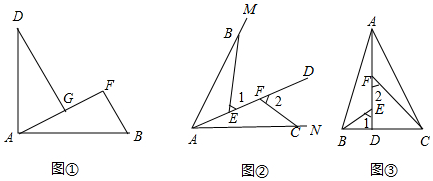
發(fā)布：2025/5/24 23:0:1組卷：156引用：2難度：0.3 -
3．在△ABC中，AB=BC，∠B=45°，AD為BC邊上的高，M為線段AB上一動(dòng)點(diǎn)．
（1）如圖1，連接CM交AD于Q，若∠ACM=45°，AB=．求線段DQ的長(zhǎng)度；2
（2）如圖2，點(diǎn)M，N在線段AB上，且AM=BN，連接CM，CN分別交線段AD于點(diǎn)Q、P，若點(diǎn)P為線段CN的中點(diǎn)，求證：AQ+CD=AB；2
（3）如圖3，若AD=4，當(dāng)點(diǎn)M在運(yùn)動(dòng)過(guò)程中，射線DB上有一點(diǎn)G，滿足BM=10DG，AG+2MG的最小值．55
發(fā)布：2025/5/24 23:0:1組卷：102引用：1難度：0.1