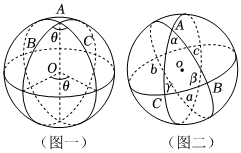
 如圖一:球面上的任意兩個(gè)與球心不在同一條直線上的點(diǎn)和球心確定一個(gè)平面,該平面與球相交的圖形稱為球的大圓,任意兩點(diǎn)都可以用大圓上的劣弧進(jìn)行連接.過球面一點(diǎn)的兩個(gè)大圓弧,分別在弧所在的兩個(gè)半圓內(nèi)作公共直徑的垂線,兩條垂線的夾角稱為這兩個(gè)弧的夾角.
如圖一:球面上的任意兩個(gè)與球心不在同一條直線上的點(diǎn)和球心確定一個(gè)平面,該平面與球相交的圖形稱為球的大圓,任意兩點(diǎn)都可以用大圓上的劣弧進(jìn)行連接.過球面一點(diǎn)的兩個(gè)大圓弧,分別在弧所在的兩個(gè)半圓內(nèi)作公共直徑的垂線,兩條垂線的夾角稱為這兩個(gè)弧的夾角.
如圖二:現(xiàn)給出球面上三個(gè)點(diǎn),其任意兩個(gè)不與球心共線,將它們兩兩用大圓上的劣弧連起來的封閉圖形稱為球面三角形.兩點(diǎn)間的弧長定義為球面三角形的邊長,兩個(gè)弧的夾角定義為球面三角形的角.
現(xiàn)設(shè)圖二球面三角形ABC的三邊長為a,b,c,三個(gè)角大小為α,β,γ,球的半徑為R.
(1)求證:a+b>c
(2)①求球面三角形ABC的面積S(用α,β,γ,R表示).
②證明:α+β+γ>π.
【考點(diǎn)】球的體積和表面積.
【答案】(1)證明見解析;
(2)①S=(α+β+γ-π)R2;
②證明見解析.
(2)①S=(α+β+γ-π)R2;
②證明見解析.
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/7/17 8:0:9組卷:41引用:3難度:0.6
相似題
-
1.大約于東漢初年成書的我國古代數(shù)學(xué)名著《九章算術(shù)》中,“開立圓術(shù)”曰:置積尺數(shù),以十六乘之,九而一,所得開立方除之,即立圓徑.“開立圓術(shù)”實(shí)際是知道了球的體積V,利用球的體積,求其直徑d的一個(gè)近似值的公式
,而我們知道,若球的半徑r,則球的體積d=3169V,則在上述公式V=43πr3中,相當(dāng)于π的取值為( )d=3169VA.3 B. 227C. 278D. 169發(fā)布:2024/12/30 4:0:3組卷:71引用:2難度:0.6 -
2.正方體的表面積與其外接球的表面積的比為( )
A.3:π B.2:π C.1:2π D.1:3π 發(fā)布:2024/12/29 12:30:1組卷:9引用:3難度:0.7 -
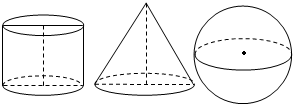 3.如圖,一個(gè)圓柱和一個(gè)圓錐的底面直徑和它們的高都與一個(gè)球的直徑2R相等,下列結(jié)論正確的是( )
3.如圖,一個(gè)圓柱和一個(gè)圓錐的底面直徑和它們的高都與一個(gè)球的直徑2R相等,下列結(jié)論正確的是( )A.圓柱的側(cè)面積為4πR2 B.圓錐的側(cè)面積為 5πR2C.圓柱的側(cè)面積與球面面積相等 D.三個(gè)幾何體的表面積中,球的表面積最小 發(fā)布:2024/12/29 9:0:1組卷:352引用:11難度:0.8
相關(guān)試卷


