當前位置:
試題詳情
參照學習函數的過程與方法,探究函數y=x-2x(x≠0)的圖象與性質.因為y=x-2x=1-2x,即y=-2x+1,所以我們對函數y=-2x來探究.列表:
y
=
x
-
2
x
(
x
≠
0
)
y
=
x
-
2
x
=
1
-
2
x
y
=
-
2
x
+
1
y
=
-
2
x
| x | … | -4 | -3 | -2 | -1 | - 1 2 |
1 2 |
1 | 2 | 3 | 4 | … |
y = - 2 x |
… | 1 2 |
2 3 |
1 | 2 | 4 | -4 | -2 | -1 | - 2 3 |
- 1 2 |
… |
y = x - 2 x |
… | 3 2 |
5 3 |
m | 3 | 5 | -3 | -1 | n | 1 3 |
1 2 |
… |
(1)仿照函數
y
=
-
2
x
y
=
x
-
2
x
(
x
≠
0
)
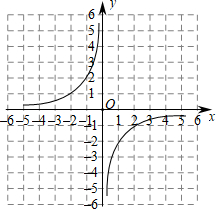
①補全表格:m=
2
2
,n=0
0
.②根據表格,在平面直角坐標系中描出點(-2,m)和(2,n),并繪制函數
y
=
x
-
2
x
(
x
≠
0
)
觀察
y
=
x
-
2
x
(
x
≠
0
)
③當x<0時,y隨x的增大而
增大
增大
(填“增大”或“減小”).④函數
y
=
x
-
2
x
y
=
-
2
x
上
上
平移 1
1
個單位長度得到的.(2)請在網格中直接畫出直線y=-x的圖象,結合函數、不等式之間的關系直接寫出不等式
x
-
2
x
≤
-
x
x≤-2或0<x≤1
x≤-2或0<x≤1
.【考點】反比例函數與一次函數的交點問題.
【答案】2;0;增大;上;1;x≤-2或0<x≤1
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/5/23 20:19:40組卷:99引用:3難度:0.6
相似題
-
 1.如圖,直線y=2x+6與反比例函數y=(??>0)的圖象交于點A(1,m),與x軸交于點B,平行于x軸的直線y=n(0<n<6)交反比例函數的圖象于點M,交AB于點N,連接BM.kx
1.如圖,直線y=2x+6與反比例函數y=(??>0)的圖象交于點A(1,m),與x軸交于點B,平行于x軸的直線y=n(0<n<6)交反比例函數的圖象于點M,交AB于點N,連接BM.kx
(1)求m的值和反比例函數的表達式;
(2)觀察圖象,直接寫出當x>0時,不等式2x+6<0的解集;-kx
(3)當n為何值時,△BMN的面積最大?最大值是多少?發布:2025/6/10 5:0:1組卷:1673引用:5難度:0.4 -
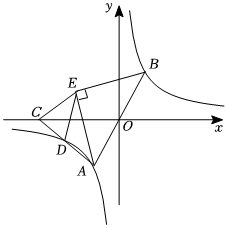 2.如圖,過原點的直線與反比例函數y=(k>0)交于A、B兩點,點A在第三象限,點C在x軸的負半軸上,連AC交反比例函數于點D,AE為∠CAB的角平分線,過點B作BE⊥AE,連DE,若D為AC中點,△ADE面積為12,則k的值為 .kx發布:2025/6/10 4:0:1組卷:182引用:1難度:0.4
2.如圖,過原點的直線與反比例函數y=(k>0)交于A、B兩點,點A在第三象限,點C在x軸的負半軸上,連AC交反比例函數于點D,AE為∠CAB的角平分線,過點B作BE⊥AE,連DE,若D為AC中點,△ADE面積為12,則k的值為 .kx發布:2025/6/10 4:0:1組卷:182引用:1難度:0.4 -
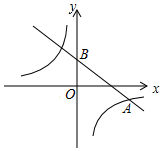 3.在平面直角坐標系中,一次函數y=-x+b的圖象與y軸交于點B(0,2),與反比例函數y=34的圖象交于點A(4,-1).mx
3.在平面直角坐標系中,一次函數y=-x+b的圖象與y軸交于點B(0,2),與反比例函數y=34的圖象交于點A(4,-1).mx
(1)求反比例函數的表達式和一次函數表達式;
(2)如果點P是x軸上的一點,且△ABP的面積是3,求P點的坐標.發布:2025/6/10 5:0:1組卷:120引用:2難度:0.5


