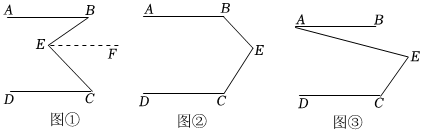
（1）問題發現：如圖①，直線AB∥CD，E是AB與AD之間的一點，連接BE，CE，可以發現∠B+∠C=∠BEC．請把下面的說理過程補充完整：解：過點E作EF∥AB，因為AB∥DC（已知），EF∥AB，所以EF∥DC，（ 平行于同一直線的兩直線平行平行于同一直線的兩直線平行）所以∠C=∠CEF∠CEF.（ 兩直線平行，內錯角相等兩直線平行，內錯角相等）因為EF∥AB，所以∠B=∠BEF∠BEF，所以∠B+∠C=∠BEF+∠CEF．即∠B+∠C=∠BEC．
（2）拓展探究：如果點E運動到圖②所示的位置，其他條件不變，則∠B、∠C、∠BEC的關系為 ∠B+∠C=360°-∠BEC∠B+∠C=360°-∠BEC.（直接寫出結論，不用說明理由）
（3）解決問題：如圖③，AB∥DC，∠C=120°，∠AEC=80°，則∠A=20°20°.（直接寫出結果，不用寫計算過程）
?
【答案】平行于同一直線的兩直線平行；∠CEF；兩直線平行，內錯角相等；∠BEF；∠B+∠C=360°-∠BEC；20°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/27 8:0:10組卷：92引用：1難度：0.7
相似題
-
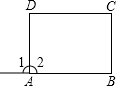1．如圖，已知∠1=∠B，∠2=∠C，則下列結論不成立的是（ ）發布：2025/6/8 17:30:2組卷：143引用：13難度：0.9 -
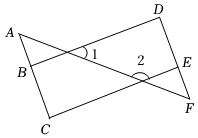2．補全下面的解題過程（填理由或數學式）．
如圖，∠1=50°，∠2=130°，∠C=∠D．求∠A與∠F的數量關系．
解：∵∠1=50°，∠2=130°（已知），
∴∠1+∠2=°．
∴BD∥（ ）．
∴∠C=∠ABD （ ）．
∵∠C=∠D（已知），
∴∠ABD=∠（等量代換），
∴AC∥DF （ ），
∴∠A=∠F （ ）．發布：2025/6/8 17:30:2組卷：431引用：8難度：0.6 -
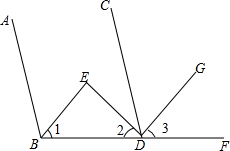3．如圖，BE平分∠ABD，DE平分∠BDC，DG平分∠CDF，且∠1+∠2=90°，試說明BE∥DG．發布：2025/6/8 17:30:2組卷：640引用：2難度：0.5