數學興趣小組的同學發現：如果∠1+∠2=45°，那么當∠1所對的直角邊與另一直角邊比值一定時，∠2所對的直角邊與另一直角邊也存在一定的數量關系．
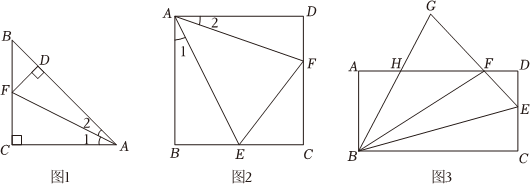
（1）嘗試：①如圖1，在等腰直角△ABC中，∠ACB=90°，AC=4，點F是BC的中點，DF⊥AB于點D，連接AF，則CFAC=1212，DFAD=1313；
②如圖2，在正方形ABCD中，AB=2，點E為BC中點，∠EAF=45°，求DFAD的值；
（2）推理：如圖2，在正方形ABCD中，AB=a,保留②中其他條件不變，DFAD的值；
（3）運用：如圖3，在矩形ABCD的CD邊上取一點E，將△BCE沿BE翻折，使點C恰好落在AD邊上的點F處，延長EF，與∠ABF的角平分線交于點G，BG交AD于點H．當AB=4，AH=2，DF=43時，求BG的長．
CF
AC
1
2
1
2
DF
AD
1
3
1
3
DF
AD
DF
AD
DF
=
4
3
【考點】相似形綜合題．
【答案】；
1
2
1
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/30 8:0:9組卷：524引用：4難度：0.1
相似題
-
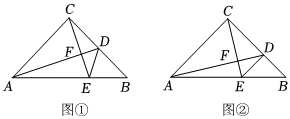1．如圖①，在Rt△ABC中，AC=BC，∠ACB=90°，點D為BC邊上的一點，連接AD，過點C作CE⊥AD于點F，交AB于點E，連接DE．
（1）若AE=2BE，求證：AF=2CF；
（2）如圖②，若AB=，DE⊥BC，求2的值．BEAE發布：2025/5/24 7:30:1組卷：247引用：4難度：0.2 -
2．（1）如圖①，在正方形ABCD中，E，F分別是AB，BC邊上的動點，且∠EDF=45°，將△DAE繞點D逆時針旋轉90°，得到△DCM，可以證明△DEF≌△DMF，進一步推出EF，AE，FC之間的數量關系為 ；
（2）在圖①中，連接AC分別交DE和DF于P，Q兩點，求證：△DPQ∽△DFE；
（3）如圖②，在菱形ABCD中，∠ABC=60°，點E，F分別是邊BC，CD上的動點（不與端點重合），且∠EAF=60°，連接BD分別與邊AE，AF交于M，N．當∠DAF=15°時，猜想MN，DN，BM之間存在什么樣的數量關系，并證明你的結論．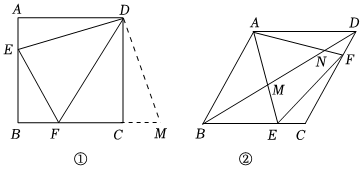
發布：2025/5/24 8:0:1組卷：711引用：2難度：0.1 -
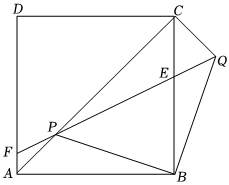3．如圖，正方形ABCD的邊長為2，P是對角線AC上的一個動點（不與A、C重合），連接BP，以BP為直角邊作等腰直角△BPQ，BQ⊥BP，QP交BC于點E，QP延長線與邊AD交于點F．2
（1）連接CQ，求證：AP=CQ；
（2）求證：△ABP∽△CPE；
（3）設AP=x,CE=y,試寫出y關于x的函數關系式，并求當CE=BC時，x的值．38發布：2025/5/24 8:30:1組卷：236引用：1難度：0.1