在平面直角坐標系xOy中,對于任意兩點P1(x1,y1)與P2(x2,y2),我們重新定義這兩點的“距離”.
①當|y1-y2|≤|x1-x2|時,|x1-x2|為點P1與點P2的“遠距離”D遠,即D遠(P1,P2)=|x1-x2|;當|x1-x2|<|y1-y2|時,|y1-y2|為點P1與點P2的“遠距離”D遠,即D遠(P1,P2)=|y1-y2|.
②點P1與點P2的“總距離”D總為|x1-x2|與|y1-y2|的和,即D總(P1,P2)=|x1-x2|+|y1-y2|.
根據以上材料,解決下列問題:
(1)已知點A(3,2),則D遠(A,O)=33;D總(A,O)=55.
(2)若點B(x,5-x)在第一象限,且D遠(B,O)=3.求點B的坐標.
(3)①若點C(x,y)(x≥0,y≥0),且D總(C,O)=4,所有滿足條件的點C組成了圖形W,請在圖一中畫出圖形W;
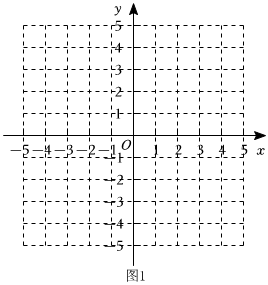
②已知點M(m,0),N(m+1,2),若在線段MN上存在點E,使得點E滿足D遠(E,O)≤4且D總(E,O)≥4,請直接寫出m的取值范圍.
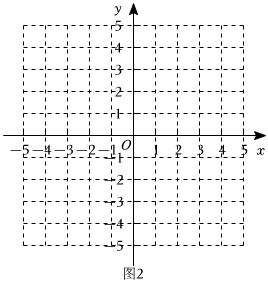
【答案】3;5
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/10 7:30:1組卷:211引用:2難度:0.4


