百錢買百雞問(wèn)題是記載于中國(guó)古代5—6世紀(jì)成書(shū)的《張邱建算經(jīng)》中的一道不定方程組問(wèn)題，其重要之處在于開(kāi)創(chuàng)“一問(wèn)多答”的先例，這是過(guò)去中國(guó)古算書(shū)中所沒(méi)有的。其問(wèn)題是這樣的：今有雞翁一，值錢伍；雞母一，值錢三；雞雛三，值錢一。凡百錢買雞百只，問(wèn)雞翁、母、雛各幾何？
用偽代碼描述解決不定方程組5i+3j+k/3=100 i+j+k=100
的正整數(shù)解的算法如下：
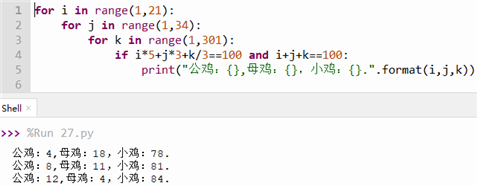
（1）該算法采用的是 窮舉法/枚舉法窮舉法/枚舉法（選填“窮舉法”、“解析法”、“枚舉法”、“分治法”）。
（2）該算法中，條件i*5+j*3+k/3==100 and i+j+k==100共被判斷了多少次？（可以直接填計(jì)算結(jié)果也可以填計(jì)算式子）。
5 i + 3 j + k / 3 = 100 |
i + j + k = 100 |
【考點(diǎn)】枚舉算法及程序?qū)崿F(xiàn)．
【答案】窮舉法/枚舉法
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：5引用：1難度：0.3
相似題
-
1．以下問(wèn)題，適合用枚舉法解決的是（ ）
發(fā)布：2024/11/8 11:30:1組卷：2引用：1難度：0.8 -
2．若一個(gè)三位數(shù)abc,滿足abc=a3+b3+c3，則稱abc為水仙花數(shù)。如三位數(shù)153滿足13+53+33=1+125+27=153，則153是水仙花數(shù)。請(qǐng)把所有滿足條件的水仙花數(shù)輸出。
（1）分析問(wèn)題。由題意可知，三位數(shù)的范圍是100～999，我們可以讓計(jì)算機(jī)一一檢查每一個(gè)三位數(shù)，輸出其中的水仙花數(shù)。設(shè)百位數(shù)字、十位數(shù)字、個(gè)位數(shù)字分別是a,b,c（0＜a≤9，0≤b≤9，0≤c≤9），這個(gè)三位數(shù)就可以表示為100×a+10×b+c,如果它正好等于各位數(shù)字的立方和，那么它就是水仙花數(shù)。
（2）設(shè)計(jì)算法。
①令a從1～9窮舉；
②令b從0～9窮舉；
③令c從0～9窮舉；
④如果100×a+10×b+c和a3+b3+c3相等，那么就把它輸出。
⑤轉(zhuǎn)步驟③，重復(fù)執(zhí)行③④⑤，直到c窮舉完畢；
⑥轉(zhuǎn)步驟②，重復(fù)執(zhí)行②③④⑤⑥，直到b窮舉完畢；
⑦轉(zhuǎn)步驟①，重復(fù)執(zhí)行①②③④⑤⑥⑦，直到a窮舉完畢；
⑧跳出循環(huán)，結(jié)束。
（3）編寫(xiě)程序。
（4）調(diào)試程序。發(fā)布：2024/8/7 8:0:9組卷：1引用：0難度：0.4 -
3．如果一個(gè)4位數(shù)恰好等于它的各位數(shù)字的4次方和，則這個(gè)數(shù)被稱為“玫瑰花”數(shù)。例如1634就是一個(gè)玫瑰花數(shù)：1634=14+64+34+44。如果要求出所有的玫瑰花數(shù)，下列算法合適的是（ ）
發(fā)布：2024/11/16 22:30:5組卷：7引用：2難度：0.5
相關(guān)試卷