【了解概念】
如圖1，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，連接CE，連接BD并延長與CE交于點F，那么將∠BFC叫做△ABC和△ADE的底聯角．
【探究歸納】
（1）兩個等腰三角形的底聯角與這兩個等腰三角形的頂角有怎樣的數量關系？請用文字語言寫出結論．
【拓展提升】
運用（1）中的結論解決問題：
（2）如圖2，AB=AC，AD=AE，∠BAC=DAE=90°，∠DCE=62°，求∠BDC的度數；
（3）如圖3，在四邊形ABCD中，AB=6，BC=4，CD=5，點O為四邊形ABCD內一點．且OA=OB，OC=OD，∠AOB=∠COD=90°，求AD的長．
【考點】四邊形綜合題．
【答案】（1）兩個等腰三角形的底聯角等于這兩個等腰三角形的頂角，理由見解答；
（2）∠BDC=152°或∠BDC=28°；
（3）AD的長為3．
（2）∠BDC=152°或∠BDC=28°；
（3）AD的長為3
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/4 1:0:8組卷：1065引用：4難度：0.3
相似題
-
1．如圖，矩形ABCD中，AB=21cm,AD=12cm.E是CD邊上的一點，DE=16cm,M是BC邊的中點，動點P從點A出發，沿邊AB以1cm/s的速度向終點B運動，過點P作PH⊥AE于點H，連接EP，設動點P的運動時間是t（s）（0＜t＜21）．
（1）求t為何值時，PM⊥EM；
（2）設△EHP的面積為y（cm2），寫出y（cm2）與t（s）之間的函數關系式；
（3）當EP平分四邊形PMEH的面積時，求t的值．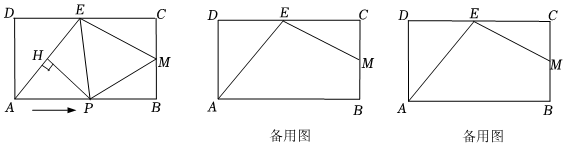
發布：2025/5/24 2:30:1組卷：100引用：1難度：0.1 -
2．綜合與實踐
綜合與實踐課上，老師與同學們以“特殊的三角形”為主題開展數學活動．
（1）操作判斷
如圖1，在△ABC中，∠ABC=90°，AB=BC，點P是直線AC上一動點．
操作：連接BP，將線段BP繞點P逆時針旋轉90°得到PD，連接DC，如圖2．
根據以上操作，判斷：如圖3，當點P與點A重合時，則四邊形ABCD的形狀是 ；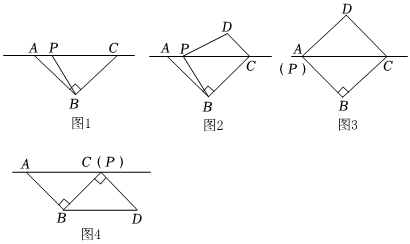
（2）遷移探究
①如圖4，當點P與點C重合時，連接DB，判斷四邊形ABDC的形狀，并說明理由；
②當點P與點A，點C都不重合時，試猜想DC與BC的位置關系，并利用圖2證明你的猜想；
（3）拓展應用
當點P與點A，點C都不重合時，若AB=4，AP=3，請直接寫出CD的長．發布：2025/5/24 2:30:1組卷：193引用：1難度：0.2 -
3．（1）證明推斷
如圖1，在正方形ABCD中，點E是對角線BD上一點，過點E作AE，BD的垂線，分別交直線BC于點F、G．
①求證：△ABE≌△FGE；
②推斷：的值為 ；EFAE
（2）類比探究
如圖2，在矩形ABCD中，=m,點E是對角線BD上一點，過點E作AE，BD的垂線分別交直線BC于點F，G．探究ABBC的值（用含m的式子表示），并寫出探究過程；EFAE
（3）拓展運用
在（2）的條件下，連接CE，當m=，CE=CD時，若CG=1，求EF的長．12
發布：2025/5/24 2:30:1組卷：739引用：4難度：0.1