綜合與實踐：
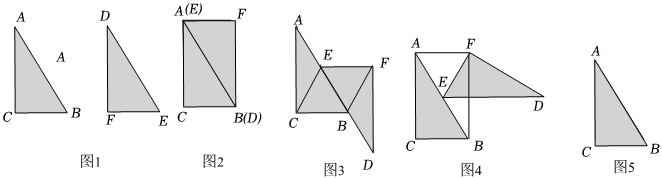
問題背景：在一次綜合與實踐課上，老師讓同學們以兩個全等的三角形紙片為操作對象，進行相關問題的研究，下面是創新小組在操作紙片過程中研究的問題，請你解決這些問題．如圖1，△ABC≌△DEF，其中∠ACB=90°，∠ABC=60°，BC=2，AB=2BC，．
操作與發現：
（1）如圖2，創新小組將兩張三角形紙片按如圖所示的方式放置后，經過觀察發現四邊形ACBF是矩形，請你證明這個結論．
操作與探究：
（2）創新小組在圖2的基礎上，將△DEF紙片沿AB方向平移至如圖3的位置，其中點E與AB的中點重合，連接CE，BF，經過探究后發現四邊形BCEF是菱形，請你證明這個結論．
（3）創新小組在圖3的基礎上又進行了探究，將△DEF紙片繞點E逆時針旋轉至DE與BC平行的位置，如圖4所示，連接AF，BF．創新小組經過觀察與推理后發現四邊形ACBF是矩形，請你證明這個結論．
提出問題：
（4）請你參照以上操作，在圖2的基礎上，通過平移或旋轉△DEF構造出的圖形，在圖5中畫出這個圖形，標明字母，說明構圖方法，寫出你發現的結論，不必證明．
【考點】四邊形綜合題．
【答案】（1）證明見解答；
（2）證明見解答；
（3）證明見解答；
（4）將△DEF向下平移DF的長度，得到四邊形ACDB為平行四邊形．
（2）證明見解答；
（3）證明見解答；
（4）將△DEF向下平移DF的長度，得到四邊形ACDB為平行四邊形．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/7 8:0:9組卷：120引用：4難度：0.3
相似題
-
1．如圖所示，在平行四邊形ABCD中，∠DAC=60°，點E是BC邊上一點，連接AE，AE=AB，點F是對角線AC邊上一動點，連接EF．
（1）如圖1，若點F與對角線交點O重合，已知BE=4，OC：EC=5：3，求AC的長度；
（2）如圖2，若EC=FC，點G是AC邊上一點，連接BG、EG，已知∠AEG=60°，∠AGB+∠BCD=180°，求證：BG+EG=DC．
（3）如圖3，若BE=4，CE=，將EF繞點E逆時針旋轉90°得EF'，請直接寫出當AF'+433BF'取得最小值時△ABF′的面積．12
發布：2025/6/21 23:30:2組卷：402引用：1難度：0.4 -
2．平行四邊形ABCD中，AB⊥AC，點E在邊AD上，連BE．
（1）如圖1，AC交BE于點G，若BE平分∠ABC，且∠DAC=30°，CG=2，請求出四邊形EGCD的面積；
（2）如圖2，點F在對角線AC上，且AF=AB，連BF，過點F作FH⊥BE于H，連AH并延長交CD于點M，點N在邊AD上，連MN．若AN=BF，2∠NMD=∠DAC+∠HBF，求證：HF+AH=AC．2
（3）如圖3，線段PO在線段BE上運動，點R在邊BC上，連接CQ、PR．若BE平分∠ABC，∠DAC=30°，AB=，PQ=3，BC=4BR．請直接寫出線段CQ+PQ+PR的和的最小值以及此時△CQE的面積．32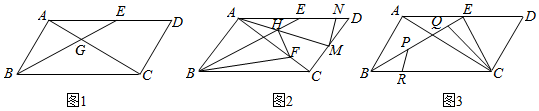
發布：2025/6/22 1:0:1組卷：261引用：3難度：0.5 -
3．如圖，四邊形ABCD是平行四邊形，點E、F在BC上，且CF=BE，連接DE，過點F作FG⊥AB于點G．
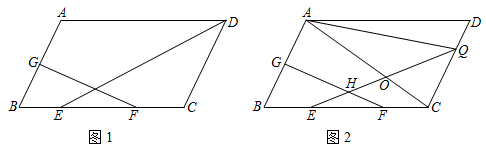
（1）如圖1，若∠B=60°，DE平分∠ADC，且CD=2CF，CD=6，求平行四邊形ABCD的面積．3
（2）點H在GF上，且HE=HF，延長EH交AC，CD于點O，Q，連接AQ，若AC=BC=EQ，∠EQC=45°，求證：CE=BG+DQ．2發布：2025/6/21 23:0:2組卷：155引用：1難度：0.1