 閱讀下面題目及其解答過程.
閱讀下面題目及其解答過程.
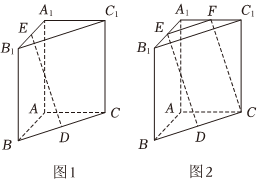
如圖1,在直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分別為BC,A1B1的中點.
(1)求證:DE∥平面A1ACC1;
(2)求證:AB⊥DE.
解:(1)取A1C1的中點F,連接EF,FC,如圖2所示.
在△A1B1C1中,E,F分別為A1B1,A1C1的中點,
所以EF∥B1C1,EF=12B1C1.
由題意知,四邊形B1BCC1為①.
因為D為BC的中點,所以DC∥B1C1,DC=12B1C1.
所以EF∥DC,EF=DC.
所以四邊形DCFE為平行四邊形,
所以DE∥CF.
又②,CF?平面A1ACC1,
所以,DE∥平面A1ACC1.
(2)因為ABC-A1B1C1為直三棱柱,所以A1A⊥平面ABC.
又AB?平面ABC,所以③.
因為AB⊥AC,且A1A⊥AC=A,所以④.
又CF?平面A1ACC1,所以AB⊥CF.
因為⑤,所以AB⊥DE.
以上題目的解答過程中,設置了①~⑤五個序號,如下的表格中為每個序號給出了兩個選項,其中只有一個符合邏輯推理.請選出符合邏輯推理的選項(只需填寫“A”或“B”).
EF
=
1
2
B
1
C
1
DC
=
1
2
B
1
C
1
| 序號 | 選項 |
| ① | A.矩形????????B.梯形 |
| ② | A.DE?平面A1ACC1??B.DE?平面A1ACC1 |
| ③ | A.BC⊥A1A??????B.AB⊥A1A |
| ④ | A.AB⊥平面A1ACC1??B.BC⊥平面A1ACC1 |
| ⑤ | A.DE=CF???????B.DE∥CF |
【答案】(1)①A;②A;(2)③B;④A;⑤B.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/10/25 0:0:1組卷:49引用:2難度:0.7
相似題
-
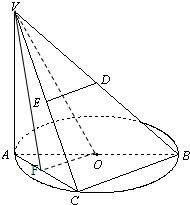 1.如圖,AB是圓O的直徑,點C是弧AB的中點,D、E、F分別是VB,VC,AC的中點,VA⊥平面ABC.
1.如圖,AB是圓O的直徑,點C是弧AB的中點,D、E、F分別是VB,VC,AC的中點,VA⊥平面ABC.
(Ⅰ)求證:DE∥平面VOF;
(Ⅱ)求證:DE⊥平面VAC.發布:2025/1/20 8:0:1組卷:27引用:1難度:0.5 -
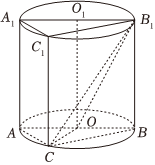 2.如圖,圓柱OO1內有一個三棱柱ABC-A1B1C1,三棱柱的底面為圓柱底面的內接三角形,且AB是圓O的直徑.
2.如圖,圓柱OO1內有一個三棱柱ABC-A1B1C1,三棱柱的底面為圓柱底面的內接三角形,且AB是圓O的直徑.
(1)證明:O1A∥平面B1OC;
(2)證明:平面A1ACC1⊥平面B1BCC1;
(3)設AB=AA1=2,在圓柱OO1內隨機選取一點,記該點取自于三棱柱ABC-A1B1C1內的概率為P,當點C在圓周上運動時,求P的最大值.發布:2025/1/20 8:0:1組卷:25引用:1難度:0.3 -
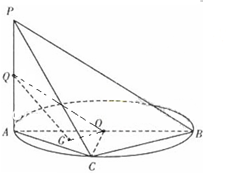 3.如圖,AB是圓O的直徑,C是圓O上的點.P是圓所在的面外一點.設Q為PA的中點,G為AOC的重心.求證:QG∥平面PBC.發布:2025/1/20 8:0:1組卷:81引用:0難度:0.7
3.如圖,AB是圓O的直徑,C是圓O上的點.P是圓所在的面外一點.設Q為PA的中點,G為AOC的重心.求證:QG∥平面PBC.發布:2025/1/20 8:0:1組卷:81引用:0難度:0.7


