閱讀材料:根據多項式乘多項式法則,我們很容易計算:
(x+2)(x+3)=x2+5x+6;(x-1)(x+3)=x2+2x-3.
而因式分解是與整式乘法方向相反的變形,利用這種關系可得:
x2+5x+6=(x+2)(x+3);x2+2x-3=(x-1)(x+3).
通過這樣的關系我們可以將某些二次項系數是1的二次三項式分解因式.如將式子x2+2x-3分解因式.這個式子的二次項系數是1=1×1,常數項-3=(-1)×3,一次項系數2=(-1)+3,可以用圖中十字相乘的形式表示為:
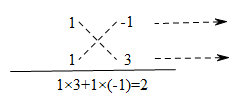
先分解二次項系數,分別寫在十字交叉線的左上角和左下角;再分解常數項,分別寫在十字交叉線的右上角和右下角;然后交叉相乘,求和,使其等于一次項系數,然后橫向書寫.這樣,我們就可以得到:x2+2x-3=(x-1)(x+3).
利用這種方法,將下列多項式分解因式:
(1)x2+7x+10=(x+2)(x+5)(x+2)(x+5);
(2)x2-2x-3=(x-3)(x+1)(x-3)(x+1);
(3)y2-7y+12=(y-3)(y-4)(y-3)(y-4);
(4)x2+7x-18=(x+9)(x-2)(x+9)(x-2).
【考點】因式分解-十字相乘法等.
【答案】(x+2)(x+5);(x-3)(x+1);(y-3)(y-4);(x+9)(x-2)
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/9 23:0:1組卷:2904引用:3難度:0.5
相似題
-
1.若x2-nx-6=(x-2)(x+3),則常數n的值是 .
發布:2025/6/9 2:30:1組卷:356引用:3難度:0.7 -
2.對于形如x2+2ax+a2這樣的二次三項式,可以用公式法將它分解成(x+a)2的形式.但對于二次三項式x2+2ax-3a2,就不能直接運用公式了.此時,我們可以在二次三項式x2+2ax-3a2中先加上一項a2,使它與x2+2ax的和成為一個完全平方式,再減去a2,整個式子的值不變,于是有:
x2+2ax-3a2=(x2+2ax+a2)-a2-3a2
=(x+a)2-(2a)2
=(x+3a)(x-a).
像這樣,先添一適當項,使式中出現完全平方式,再減去這個項,使整個式子的值不變的方法稱為“配方法”.
(1)利用“配方法”分解因式:
①a2-6a-7;
②a4+a2b2+b4.
(2)若a+b=5,ab=6,求:
①a2+b2;
②a4+b4的值.發布:2025/6/8 21:0:2組卷:192引用:3難度:0.5 -
3.若x2+mx-15=(x+3)(x+n),則m-n的值為.
發布:2025/6/9 2:30:1組卷:1994引用:5難度:0.5


