如果從一個(gè)多邊形的一個(gè)頂點(diǎn)出發(fā)作它的對角線，最多能將多邊形分成6個(gè)三角形，那么這個(gè)多邊形是（　　）

A．6邊形

B．7邊形

C．8邊形

D．9邊形

【答案】C

【解答】

【點(diǎn)評】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2024/8/19 0:0:1組卷：29引用：3難度：0.5

相似題

1．大自然中有許多小動(dòng)物都是“小數(shù)學(xué)家”，如圖1，蜜蜂的蜂巢結(jié)構(gòu)非常精巧、實(shí)用而且節(jié)省材料，多名學(xué)者通過觀測研究發(fā)現(xiàn)：蜂巢巢房的橫截面大都是正六邊形．如圖2，一個(gè)巢房的橫截面為正六邊形ABCDEF，若對角線AD的長約為8mm,則正六邊形ABCDEF的邊長為（　　）
A．2mm B．2
2
mm C．2
3
mm D．4mm
發(fā)布：2025/5/24 11:0:1組卷：1332引用：22難度：0.5
解析
2．一個(gè)n邊形從一個(gè)頂點(diǎn)出發(fā)最多引出7條對角線，則n的值為
．
發(fā)布：2025/5/24 0:30:1組卷：515引用：3難度：0.8
解析

3．歐拉是18世紀(jì)瑞士著名的數(shù)學(xué)家，他發(fā)現(xiàn)不論什么形狀的凸多面體．其頂點(diǎn)數(shù)（V）、面數(shù)（F）、棱數(shù)（E）之間存在的一個(gè)固定的關(guān)系式，被稱為多面體歐拉定理．請你觀察下列幾種簡單多面體模型，解答下列問題．
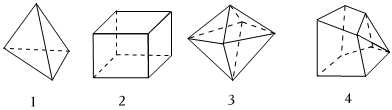
（1）【公式發(fā)現(xiàn)】根據(jù)上面的多面體模型，完成表格中的空格：

多面體編號(hào) 頂點(diǎn)數(shù)（V）面數(shù)（F）棱數(shù)（E）

1 4 4 6

2 8 6 12

3 6 8 12

4 9 8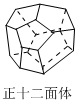

你發(fā)現(xiàn)頂點(diǎn)數(shù)（V）、面數(shù)（F）和棱數(shù)（E）之間存在的關(guān)系式是
．
（2）[公式運(yùn)用]如圖請計(jì)算正十二面體的頂點(diǎn)數(shù)和棱數(shù)．
（3）[公式綜合]已知某個(gè)玻璃飾品的外形是簡單多面體，它的外表面是由三角形和六邊形兩種多邊形排接而成，且有18個(gè)頂點(diǎn)，每個(gè)頂點(diǎn)處都有4條棱，設(shè)該多面體外表面三角形的個(gè)數(shù)為m個(gè)，六邊形的個(gè)數(shù)為n個(gè)，求m+n的值．
（4）[定理應(yīng)用]有一種足球是由數(shù)塊黑白相間的牛皮縫制而成，黑皮為正五邊形，白皮為正六邊形，且邊長都相等，請利用歐拉公式分別求出正五邊形、正六邊形個(gè)數(shù)．

發(fā)布：2025/5/24 15:30:1組卷：143引用：1難度：0.3

相關(guān)試卷