我們知道，三角形的中位線平行于三角形的第三邊，并且等于第三邊的一半，如何證明三角形中位線定理呢？
（1）【方法回顧】
證明：三角形中位線定理．
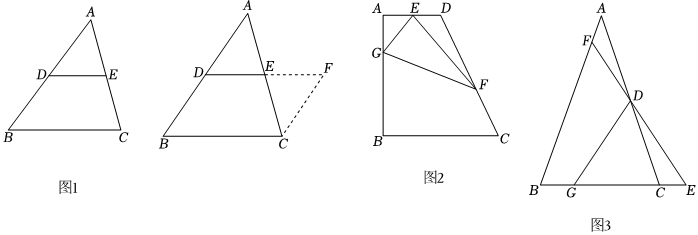
已知：如圖，在△ABC中，D、E分別是AB、AC的中點(diǎn)．
求證：DE∥BC，DE=12BC．
證明三角形中位線性質(zhì)定理的方法很多，但多數(shù)都需要通過添加輔助線構(gòu)圖去完成，下面是其中一種證法的添加輔助線方法，閱讀并完成填空：
添加輔助線，如圖1，在△ABC中，過點(diǎn)C作CF∥AB，與DE的延長(zhǎng)線交于點(diǎn)F．可證△ADE≌△CFE△CFE，根據(jù)全等三角形對(duì)應(yīng)邊相等可得DE=EF，然后判斷出四邊形BCFD是 平行四邊形平行四邊形，根據(jù)圖形性質(zhì)可證得DE∥BC，DE=12BC．
（2）【方法遷移】
如圖2，在四邊形ABCD中，AD∥BC，∠A=90°，∠D=120°，E為AD的中點(diǎn)，G、F分別為AB、CD邊上的點(diǎn)，若AG=3，DF=4，∠GEF=90°，求GF的長(zhǎng)．
（3）【定理應(yīng)用】
如圖3，在△ABC中，AB=AC，D是AC的中點(diǎn)，G是邊BC上一點(diǎn)，CGBG=K（K＞1），延長(zhǎng)BC至點(diǎn)E，使DE=DG，延長(zhǎng)ED交AB于點(diǎn)F，直接寫出ABAF的值（用含K的式子表示）．
DE
=
1
2
BC
DE
=
1
2
BC
AG
=
3
CG
BG
=
K
（
K
＞
1
）
AB
AF
【考點(diǎn)】相似形綜合題．
【答案】△CFE；平行四邊形
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/28 8:51:19組卷：584引用：3難度：0.3
相似題
-
1．【了解概念】
在凸四邊形中，若一邊與它的兩條鄰邊組成的兩個(gè)內(nèi)角相等，則稱該四邊形為鄰等四邊形，這條邊叫做這個(gè)四邊形的鄰等邊．
【理解運(yùn)用】
（1）鄰等四邊形ABCD中，∠A=30°，∠B=70°，則∠C的度數(shù)為．
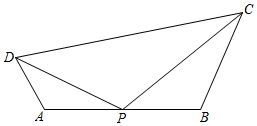
（2）如圖，凸四邊形ABCD中，P為AB邊的中點(diǎn)，△ADP∽△PDC，判斷四邊形ABCD是否為鄰等四邊形；并證明你的結(jié)論；
【拓展提升】
（3）在平面直角坐標(biāo)系中，AB為鄰等四邊形ABCD的鄰等邊，且AB邊與x軸重合，已知A（-1，0），C（m,2），D（2，33），若在邊AB上使∠DPC=∠BAD的點(diǎn)P有且僅有1個(gè)，請(qǐng)直接寫出m的值．3發(fā)布：2025/5/25 5:30:2組卷：860引用：3難度：0.3 -
2．如圖1，Rt△ABC中，∠A=90°，D為AB上一點(diǎn)，∠ACD=∠B．
（1）求證：AC2=AD?AB；
（2）如圖2，過點(diǎn)A作AM⊥CD于M，交BC于點(diǎn)E，若，求CDBC=12的值；AMME
（3）如圖3，N為CD延長(zhǎng)線上一點(diǎn)，連接AN、BN，若，∠NBD=2∠ACD，則tan∠ANC的值為 ．CDBN=53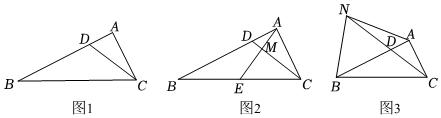
發(fā)布：2025/5/24 23:30:2組卷：239引用：1難度：0.3 -
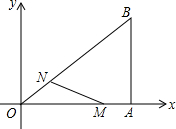3．如圖，在直角坐標(biāo)系中，Rt△OAB的直角頂點(diǎn)A在x軸上，OA=4，AB=3．動(dòng)點(diǎn)M從點(diǎn)A出發(fā)，以每秒1個(gè)單位長(zhǎng)度的速度，沿AO向終點(diǎn)O移動(dòng)；同時(shí)點(diǎn)N從點(diǎn)O出發(fā)，以每秒1.25個(gè)單位長(zhǎng)度的速度，沿OB向終點(diǎn)B移動(dòng)．當(dāng)兩個(gè)動(dòng)點(diǎn)運(yùn)動(dòng)了x秒（0＜x＜4）時(shí)，解答下列問題：
（1）求點(diǎn)N的坐標(biāo)（用含x的代數(shù)式表示）；
（2）設(shè)△OMN的面積是S，求S與x之間的函數(shù)表達(dá)式；當(dāng)x為何值時(shí)，S有最大值？最大值是多少？
（3）在兩個(gè)動(dòng)點(diǎn)運(yùn)動(dòng)過程中，是否存在某一時(shí)刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，請(qǐng)說明理由．發(fā)布：2025/5/25 2:30:1組卷：4642引用：26難度：0.5