如圖1，△ABC為等邊三角形，點E、F分別在BC和AB上，且CE=BF，AE與CF相交于點H．
（1）求證：△ACE≌△CBF；
（2）求∠CHE的度數；
（3）如圖2，在圖1上以AC為邊長再作等邊△ACD，將HE延長至G使得HG=CH，連接HD與CG，求證：HD=AH+CH．
【考點】三角形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/7 8:0:9組卷：216引用：3難度：0.1
相似題
-
1．已知△ABC中，AB=AC．
（1）如圖1，在△ADE中，若AD=AE，且∠DAE=∠BAC，求證：CD=BE；
（2）如圖2，在△ADE中，若∠DAE=∠BAC=60°，且CD垂直平分AE，AD=3，CD=4，求BD的長；
（3）如圖3，在△ADE中，當BD垂直平分AE于H，且∠BAC=2∠ADB時，試探究CD2，BD2，AH2之間的數量關系．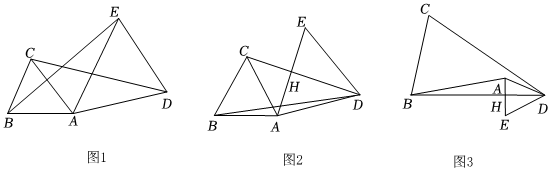
發布：2025/6/4 3:30:2組卷：262引用：1難度：0.1 -
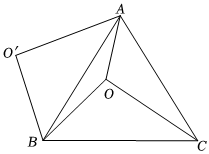2．如圖，O是正三角形ABC內一點，OA=3，OB=4，OC=5，將線段BO以點B為旋轉中心逆時針旋轉60°得到線段BO'，下列結論：
①△BO'A可以由△BOC繞點B逆時針旋轉60°得到；②點O與O'的距離為4；③∠AOB=150°④S四邊形AOBO′=6+3；⑤S△AOC+S△AOB=6+3．943
其中正確的結論是（ ）發布：2025/6/4 3:30:2組卷：215引用：2難度：0.2 -
3．在平面直角坐標系xOy中，對于點P（x,y），若點Q的坐標為（x+ay,ax+y），則稱點Q是點P的“a級跟隨點”（其中a為常數，且a≠0）．例如：點P（1，4）的“2級跟隨點”為點Q（1+2×4，2×1+4），即點Q的坐標為（9，6）．
（1）若點P的坐標（-3，5），求它的“3級跟隨點”的坐標；
（2）若點P（c+2，2c-1）先向左平移2個單位長度，在向上平移3個單位長度后得到了點P1，點P1的“-3級跟隨點”P2位于坐標軸上，求點P2的坐標．
（3）若點P在x軸正半軸上，點P的“a級跟隨點”為P3點，且線段PP3的長度為線段OP長度的2倍，求a的值．發布：2025/6/4 4:30:1組卷：95引用：1難度：0.5