【問題探究】
（1）如圖1，點A是⊙O外一點，點B在⊙O上運動，OA=4，OB=2，則AB的最小值是 22．
（2）如圖2，已知正方形ABCD的邊長為4，⊙B的半徑為2，點P是⊙B上的一個動點，求PD+12PC的最小值；
【問題解決】
（3）如圖3，四邊形ABCD是某濕地公園的鳥瞰圖，其中∠DCB=∠D=90°，AD=3千米，CD=3千米，BC=43千米，公園內有一個形狀是扇形的天然湖泊BMN，扇形BMN以BM長為半徑，BM=12BC，?MN為湖岸，其余部分為灘地．為了便于游客觀賞，公園管理方現計劃在景區中確定兩點P、Q，建玻璃棧道PQ和觀賞小路CQ，根據規劃，點P在AC右側且滿足∠APC=120°，點Q在?MN上，已知建玻璃棧道PQ每千米的造價是2萬元，建觀賞小路CQ每千米的造價是1萬元，求建玻璃棧道PQ和觀賞小路CQ至少需多少費用？（玻璃棧道以及觀賞小路的寬度忽略不計）
1
2
3
3
1
2
?
MN
?
MN
【考點】圓的綜合題．
【答案】2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：464引用：3難度：0.2
相似題
-
1．在⊙O中，直徑AB與弦CD（非直徑）交于點E，DE=CE，弦BG⊥BC交⊙O于點G，交CD于點F．
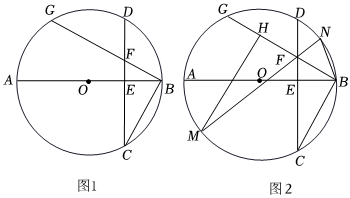
（1）如圖1，求證：∠ABF=∠BCD；
（2）如圖2，點N為弧BD上一點，連接BN、NF，并延長NF交⊙O于點M，H為FG上一點，連接MH，BN=BF，∠HMF=∠HBN，求證：FH=GH．12發布：2025/5/24 14:30:1組卷：107引用：1難度：0.1 -
2．已知在Rt△ABC中，∠C=90°，AC=
，BC=2．23
（1）如圖①，若P為BC上由點B向點C運動的一點，連接AP，設AP的中點為G，求在點P運動的過程中，點G經過的路徑長．
（2）如圖②，若P是以AB為直徑所作半圓上由點A沿著半圓向點B運動的一點，求CP的中點F經過的路徑長．
（3）如圖③，若P為BC上由點B向點C運動的一點，連接AP，作BR⊥AP于點R，（P、R可以重合）求在點P的運動過程中，R經過的路徑長．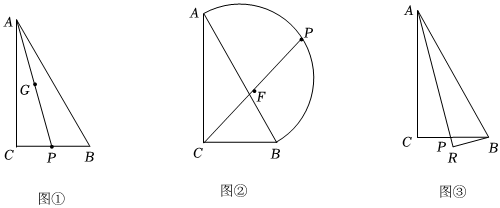
發布：2025/5/24 13:30:2組卷：86引用：1難度：0.3 -
3．如圖1，在Rt△ABC中，∠ABC=90°，以線段BC為直徑作⊙O交AC于點D，E為AB中點，連接ED，過點C作CF∥AB交ED的延長線于點F．
（1）求證：直線ED是⊙O的切線；
（2）判斷△CDF的形狀，并說明理由；
（3）如圖2，連接OF交⊙O于點P，連接BP交AC于點Q，若D為AQ中點，AB=6，求PQ的長．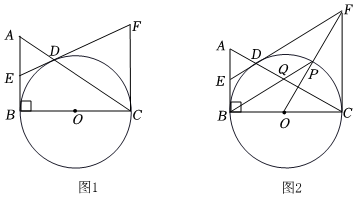
發布：2025/5/24 13:30:2組卷：319引用：2難度：0.3