（1）問題發現：
如圖①，△ABC與△ADE是等邊三角形，且點B，D，E在同一直線上，連接CE，求∠BEC的度數，并確定線段BD與CE的數量關系．
（2）拓展探究：
如圖②，△ABC與△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，且點B，D，E在同一直線上，AF⊥BE于點F，連接CE，求∠BEC的度數，并確定線段AF，BF，CE之間的數量關系．
【答案】（1）∠BEC的度數為60°；線段BD與CE之間的數量關系是：BD=CE；
（2）BF=CE+AF．
（2）BF=CE+AF．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/1 8:0:9組卷：24引用：1難度：0.5
相似題
-
1．將兩個等腰直角三角形：△ADE與△ABC（其中∠DAE=∠ABC=90°，AB=BC，AD=AE如圖放置在一起，點E在AB上，AC與DE交于點H，連接BH，CE，且∠BCE=15°下列結論：
①AC垂直平分DE；
②△CDE為等邊三角形；
③；tan∠BCD=ABBE
④．S△EBCS△EHC=13
正確的結論是（ ）發布：2025/5/23 12:30:2組卷：21引用：1難度：0.4 -
2．如圖，直線y=x-1與坐標軸交于A、B兩點，點P是曲線y=15（x＞0）上一點，若△PAB是以∠APB=90°的等腰三角形，則k=kx．發布：2025/5/23 16:30:1組卷：488引用：3難度：0.7 -
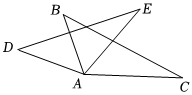3．如圖，已知AD=AB，∠D=∠B，∠DAB=∠EAC，求證：AE=AC．發布：2025/5/23 13:0:1組卷：427引用：2難度：0.5