在學習中位線時，小胖同學發現對于任意三角形，若已知一邊中點，過中點作任意一邊的平行線，則該平行線截得兩邊所成的線段為該三角形的中位線．請你補全求證內容并使用八下所學知識證明小胖同學的結論．
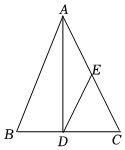
已知：在△ABC中，點E為BC中點，DE∥AC．
求證：

DE=

1

2

AC

DE=

1

2

AC

．
證明：

過點E作EF∥AD交AC于F，
∵DE∥AC，
∴四邊形ADEF是平行四邊形，
∴DE=AF，
∵點E為BC中點，EF∥AB，
∴AF=CF，
∴DE=

1

2

AC

過點E作EF∥AD交AC于F，
∵DE∥AC，
∴四邊形ADEF是平行四邊形，
∴DE=AF，
∵點E為BC中點，EF∥AB，
∴AF=CF，
∴DE=

1

2

AC

．