著名的趙爽弦圖（如圖①，其中四個直角三角形較大的直角邊長都為a,較小的直角邊長都為b,斜邊長都為c），大正方形的面積可以表示為c2，也可以表示為4×12ab+（a-b）2，由此推導出直角三角形的三邊關系：如果直角三角形兩條直角邊長為a,b,斜邊長為c,則a2+b2=c2．
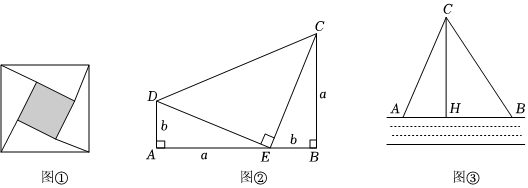
（1）圖②為美國第二十任總統伽菲爾德的“總統證法”，請你利用圖②推導上面的關系式．利用以上所得的直角三角形的三邊關系進行解答：
（2）如圖③，在一條東西走向河流的一側有一村莊C，河邊原有兩個取水點A，B，其中AB=AC，由于某種原因，由C到A的路現在已經不通，該村為方便村民取水決定在河邊新建一個取水點H（A、H、B條直線上），并新修一條路CH，且CH⊥AB．測得CH=6千米，HB=4.5千米，求新路CH比原路CA少多少千米？
（3）在第（2）問中若AB≠AC時，CH⊥AB，AC=8，BC=10，AB=12，設AH=x,求x的值．
4
×
1
2
ab
+
（
a
-
b
）
2
【考點】勾股定理的證明．
【答案】（1）見詳解；
（2）0.25；
（3）x=．
（2）0.25；
（3）x=
9
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/8 2:0:2組卷：244引用：2難度：0.5
相似題
-
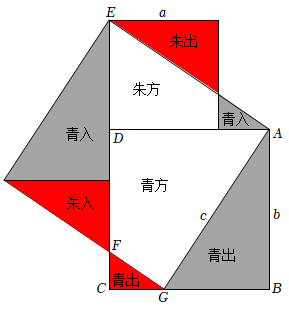
1．我國是最早了解勾股定理的國家之一，東漢末年數學家劉徽在為《九章算術》作注中依據割補術而創造了勾股定理的無字證明“青朱出入圖”，移動幾個圖形就直觀地證明了勾股定理，如圖，若a=3，b=4，則△CFG的面積為 ．
發布：2025/5/26 4:0:1組卷：110引用：1難度：0.6 -
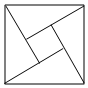2．如圖，“趙爽弦圖”是由四個全等的直角三角形和一個小正方形拼接成的大正方形，若直角三角形的兩條直角邊長分別為a,b（a＞b），大正方形的面積為S1，小正方形的面積為S2，則用含S1，S2的代數式表示（a+b）2正確的是（ ）發布：2025/5/26 4:0:1組卷：982引用：7難度：0.5 -
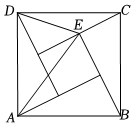3．漢代數學家趙爽為了證明勾股定理，構造了一副“弦圖”，后人稱其為“趙爽弦圖”．如圖，大正方形ABCD由四個全等的直角三角形和一個小正方形組成，若∠ADE=∠AED，，則△ADE的面積為（ ）AD=25發布：2025/5/25 11:30:2組卷：357引用：3難度：0.5