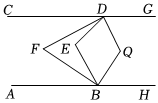
如圖，AB∥CD，∠ABF=23∠ABE，∠CDF=23∠CDE，DQ，BQ分別平分∠GDE和∠HBE，則∠DFB，∠DQB滿足的數(shù)量關系為：∠DQB+34∠DFB=180°∠DQB+34∠DFB=180°．
∠
ABF
=
2
3
∠
ABE
∠
CDF
=
2
3
∠
CDE
∠
DQB
+
3
4
∠
DFB
=
180
°
∠
DQB
+
3
4
∠
DFB
=
180
°
【考點】平行線的性質．
【答案】
∠
DQB
+
3
4
∠
DFB
=
180
°
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2025/6/10 0:0:1組卷：2322引用：4難度：0.5
相似題
-
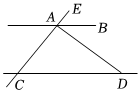1．如圖，已知直線AB∥CD，AD⊥CE，垂足為A，∠EAB=50°，則∠ADC=（ ）發(fā)布：2025/6/10 3:30:1組卷：90引用：3難度：0.7 -
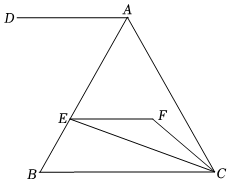2．如圖，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=124°，∠ACF=18°，求∠FEC的度數(shù)．發(fā)布：2025/6/10 3:30:1組卷：380引用：5難度：0.7 -
3．某同學在研究傳統(tǒng)文化“抖空竹”時有一個發(fā)現(xiàn)：他把它抽象成數(shù)學問題，如圖所示，已知AB∥CD，∠BAE=77°，∠DCE=131°，則∠E的度數(shù)是（ ）發(fā)布：2025/6/10 3:30:1組卷：439引用：6難度：0.8