當前位置：試題詳情

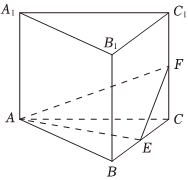如圖所示，直三棱柱ABC-A₁B₁C₁的底面是邊長為2的正三角形，E，F分別是BC，CC₁的中點．
（Ⅰ）求證：平面AEF⊥平面B₁BCC₁．
（Ⅱ）若二面角F-AE-C為45°，求三棱錐F-AEC的體積．

【答案】（Ⅰ）證明過程見解析；（Ⅱ）三棱錐F-AEC的體積為

．

【解答】

【點評】

聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。

發(fā)布：2024/7/17 8:0:9組卷：31引用：2難度：0.5

相似題

1．如圖，AB是圓O的直徑，PA垂直于圓O所在的平面，C是圓周上不同于A、B的任一點，求證：平面PAC垂直于平面PBC．
發(fā)布：2025/1/20 8:0:1組卷：48引用：1難度：0.8
解析
2．如果α⊥β，γ⊥α，β∩γ=l,那么l⊥α．

（判斷對錯）
發(fā)布：2024/7/25 8:0:9組卷：10引用：1難度：0.8
解析
3．都與第三個平面垂直的兩個平面（　　）
A．互相垂直
B．互相平行
C．相交
D．如果相交，那么交線垂直于第三個平面
發(fā)布：2024/11/10 2:30:1組卷：32引用：2難度：0.8
解析

如圖所示，直三棱柱ABC-A1B1C1的底面是邊長為2的正三角形，E，F分別是BC，CC1的中點．（Ⅰ）求證：平面AEF⊥平面B1BCC1．（Ⅱ）若二面角F-AE-C為45°，求三棱錐F-AEC的體積．