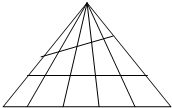
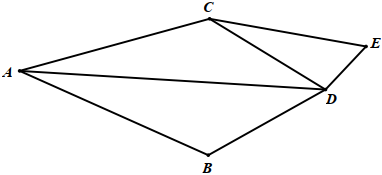
一個圖由若干個點和若干條連接這些點的線組成。如果從圖中某點出發共有n條連接線就稱n為該點的桃李值，例如，在如圖中，點A出發有3條連接線，則點A的桃李值為3；點B出發有2條線，則點B的桃李值就為2；……

（1）如果一個圖所有點的桃李值之和為2024，求這個圖連接線的數量；
（2）證明：對任意的圖，桃李值為奇數的點必為偶數個；
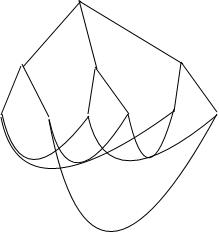
（3）一個圖，若它的每個點的桃李值均不超過3，且圖中任意兩個點或者有直接的連接線，或者總存在另外一個點與這兩個點都有連接線。請問這個圖中至多有多少個點？當點數最多時，請畫出一個這樣的圖。