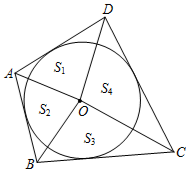
如圖，圓O是四邊形ABCD的內切圓，連接AO、BO、CO、DO，記△AOD、△AOB、△COB、△DOC的面積分別為S₁、S₂、S₃、S₄，則S₁、S₂、S₃、S₄的數量關系為
S₁+S₃=S₂+S₄
S₁+S₃=S₂+S₄
．

【答案】S₁+S₃=S₂+S₄

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/6/16 8:30:2組卷：1289引用：8難度：0.8

相似題

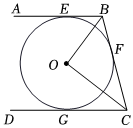1．如圖，直線AB、BC、CD分別與⊙O相切于E、F、G，且AB∥CD，OB=6cm,OC=8cm.求：
（1）∠BOC的度數；
（2）BE+CG的長；
（3）⊙O的半徑．
發布：2025/6/17 20:30:2組卷：7346引用：13難度：0.3
解析
2．如圖，⊙O為△ABC的內切圓，AC=10，AB=8，BC=9，點D，E分別為BC，AC上的點，且DE為⊙O的切線，則△CDE的周長為（　　）
A．9 B．7 C．11 D．8
發布：2025/6/17 21:30:1組卷：2486引用：12難度：0.7
解析
3．如圖，PA、PB是⊙O的切線，A、B為切點，點C、D在⊙O上．若∠P=102°，則∠A+∠C=
．
發布：2025/6/17 17:30:2組卷：6223引用：29難度：0.6
解析

相關試卷

如圖，圓O是四邊形ABCD的內切圓，連接AO、BO、CO、DO，記△AOD、△AOB、△COB、△DOC的面積分別為S1、S2、S3、S4，則S1、S2、S3、S4的數量關系為 S1+S3=S2+S4S1+S3=S2+S4．