直線MN和同側兩點AB，在MN上找一點P，使得PA+PB最小．（尺規作圖）

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/6/24 17:30:1組卷：114引用：2難度：0.5

相似題

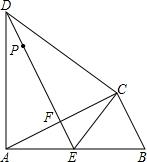1．如圖，△ABC中，∠ACB=90°，以AC為底邊作等腰三角形△ADC，AD=CD，過點D作DE⊥AC，垂足為F，DE與AB相交于點E，連接CE．AB=5，AC=4，BC=3．
（1）求證：AE=CE=BE；
（2）若P是射線DE上的一點．則當P在何處時，△PBC的周長最小，并求出此時△PBC的周長．
發布：2025/6/25 7:0:2組卷：99引用：1難度：0.3
解析
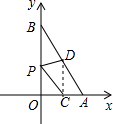2．如圖，一次函數y=kx+b的圖象與x、y軸分別交于點A（2，0）、B（0，4）．O為坐標原點，設OA、AB的中點分別為C、D，P為OB上一動點，則當P點坐標為
時，PC+PD的最小值為
．
發布：2025/6/24 14:0:1組卷：221引用：1難度：0.5
解析
3．如圖，矩形ABCD中，BC=10，∠BAC=30°，若在AC、AB上各取一點M、N，使BM+MN的值最小，求這個最小值

．
發布：2025/6/24 15:30:2組卷：817引用：2難度：0.5
解析

相關試卷

2．如圖，一次函數y=kx+b的圖象與x、y軸分別交于點A（2，0）、B（0，4）．O為坐標原點，設OA、AB的中點分別為C、D，P為OB上一動點，則當P點坐標為時，PC+PD的最小值為．