古希臘著名的畢達哥拉斯學派把1，3，6，10，…這樣的數稱為“三角形數”（如圖①），而把1，4，9，16，…這樣的數稱為“正方形數”（如圖②）． 如果規定a1=1，a2=3，a3=6，a4=10，…；b1=1，b2=4，b3=9，b4=16，…；y1=2a1+b1，y2=2a2+b2，y3=2a3+b3，y4=2a4+b4，…，那么，按此規定，y10=210210．
【考點】規律型：圖形的變化類．
【答案】210
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/24 17:30:1組卷：41引用：2難度：0.7
相似題
-
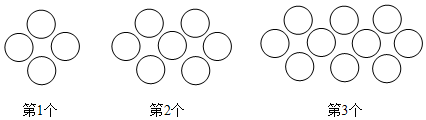
1．觀察下列圖形的構成規律，按此規律，第20個圖形中棋子的個數為 ．
發布：2025/6/25 6:30:1組卷：53引用：2難度：0.5 -
2．在同一平面內的n條直線兩兩相交，最多共有28個交點，則n=．
發布：2025/6/24 21:0:1組卷：215引用：5難度：0.7 -
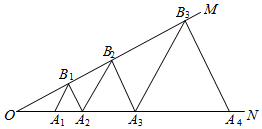3．如圖，∠MON=30°，點A1，A2，A3，A4，…在射線ON上，點B1，B2，B3，…在射線OM上，且△A1B1A2，△A2B2A3，△A3B3A4，…均為等邊三角形，以此類推，若OA1=1，則△A2021B2021A2022的邊長為．發布：2025/6/25 8:30:1組卷：662引用：9難度：0.5