小王在學習中遇到了這樣一個問題:
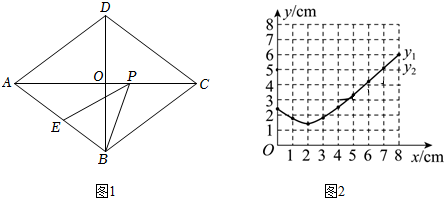
如圖1,在菱形ABCD中,對角線AC=8cm,BD=6cm,點P是AC上的動點,E是AB的中點,連接PE,PB,當△PBE是等腰三角形時,求線段AP的長度.
小王分析發現,此問題可以用函數思想解決,于是嘗試結合學習函數的經驗探究此問題.請將下面的探究過程補充完整:
根據點P在AC上的不同位置,畫出相應的圖形,測量線段AP,PE,PB的長度,得到下表的幾組對應值.
| AP/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| PE/cm | 2.5 | 1.8 | 1.5 | 1.8 | m | 3.4 | 4.3 | 5.2 | 6.2 |
| PB/cm | 5.0 | 4.2 | 3.6 | 3.2 | 3 | 3.2 | 3.6 | 4.2 | 5.0 |
2.5
2.5
;(2)將線段AP的長度作為自變量x,PE,PB的長度都是關于x的函數,分別記為y1,y2,并在平面直角坐標系xOy中畫出了y1的函數圖象,如圖2所示,請在同一平面直角坐標系中描點,并畫出y2的函數圖象.
(3)觀察圖象,可知函數y1有最小值,請你利用學習過的幾何知識,直接寫出y1的最小值.(寫出準確值)
(4)根據圖象,在點P從A移動到C的過程中,當△PBE是等腰三角形時,直接寫出AP的長.(結果精確到0.1cm)
【考點】動點問題的函數圖象.
【答案】2.5
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:365引用:5難度:0.6
相似題
-
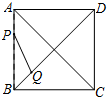 1.如圖,正方形ABCD的邊長為5,動點P的運動路線為AB→BC,動點Q的運動路線為BD.點P與Q以相同的速度分別從A,B兩點同時出發,當一個點到達終點停止運動時另一個點也隨之停止.設點P運動的路程為x,△BPQ的面積為y,則下列能大致表示y與x的函數關系的圖象為( )
1.如圖,正方形ABCD的邊長為5,動點P的運動路線為AB→BC,動點Q的運動路線為BD.點P與Q以相同的速度分別從A,B兩點同時出發,當一個點到達終點停止運動時另一個點也隨之停止.設點P運動的路程為x,△BPQ的面積為y,則下列能大致表示y與x的函數關系的圖象為( )A. 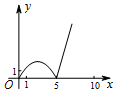
B. 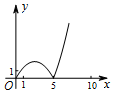
C. 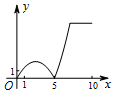
D. 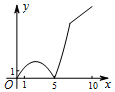 發布:2025/5/25 14:0:1組卷:805引用:7難度:0.9
發布:2025/5/25 14:0:1組卷:805引用:7難度:0.9 -
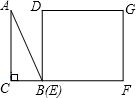 2.如圖,△ABC為直角三角形,∠C=90°,BC=2cm,∠A=30°,四邊形DEFG為矩形,,EF=6cm,且點C、B、E、F在同一條直線上,點B與點E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的邊EF向右平移,當點C與點F重合時停止.設Rt△ABC與矩形DEFG的重疊部分的面積為ycm2,運動時間xs.能反映ycm2與xs之間函數關系的大致圖象是( )DE=23cm
2.如圖,△ABC為直角三角形,∠C=90°,BC=2cm,∠A=30°,四邊形DEFG為矩形,,EF=6cm,且點C、B、E、F在同一條直線上,點B與點E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的邊EF向右平移,當點C與點F重合時停止.設Rt△ABC與矩形DEFG的重疊部分的面積為ycm2,運動時間xs.能反映ycm2與xs之間函數關系的大致圖象是( )DE=23cmA. 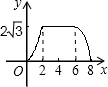
B. 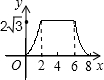
C. 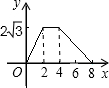
D. 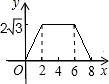 發布:2025/5/25 14:30:1組卷:4910引用:18難度:0.5
發布:2025/5/25 14:30:1組卷:4910引用:18難度:0.5 -
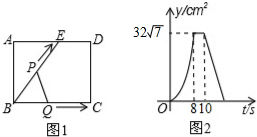 3.如圖1,E為矩形ABCD邊AD上的一點,點P從點B沿折線BE-ED-DC運動到點C時停止,點Q從點B沿BC運動到點C時停止,它們運動的速度都是2cm/s.若P、Q同時開始運動,設運動時間為t(s),△BPQ的面積為y(cm2),已知y與t的函數關系圖象如圖2,則下列結論錯誤的是( )
3.如圖1,E為矩形ABCD邊AD上的一點,點P從點B沿折線BE-ED-DC運動到點C時停止,點Q從點B沿BC運動到點C時停止,它們運動的速度都是2cm/s.若P、Q同時開始運動,設運動時間為t(s),△BPQ的面積為y(cm2),已知y與t的函數關系圖象如圖2,則下列結論錯誤的是( )A.AE=12cm B.sin∠EBC= 74C.當0<t≤8時,y= t272D.當t=9s時,△PBQ是等腰三角形 發布:2025/5/25 13:0:1組卷:742引用:47難度:0.9


