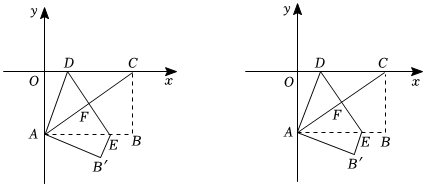
如圖，矩形OABC的兩條邊OA、OC分別在y軸和x軸上，已知點B坐標為（8，-6）．把矩形OABC沿直線DE折疊，使點C落在點A處，直線DE與OC、AC、AB的交點分別為D、F、E．
（1）線段AC=1010；
（2）求點D坐標及折痕DE的長；
（3）若點P在x軸上，在平面內是否存在點Q，使以P、D、E、Q為頂點的四邊形是菱形？若存在，則請直接寫出點Q的坐標；若不存在，請說明理由．
【考點】四邊形綜合題．
【答案】10
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/6/9 9:30:1組卷：171引用：1難度：0.1
相似題
-
1．我們定義：如果兩個等腰三角形的頂角相等，且頂角的頂點互相重合，則稱此圖形為“手拉手全等模型”．因為頂點相連的四條邊，形象的可以看作兩雙手，所以通常稱為“手拉手模型”．例如，如圖（1），△ABC與△ADE都是等腰三角形，其中∠BAC=∠DAE，則△ABD≌△ACE（SAS）
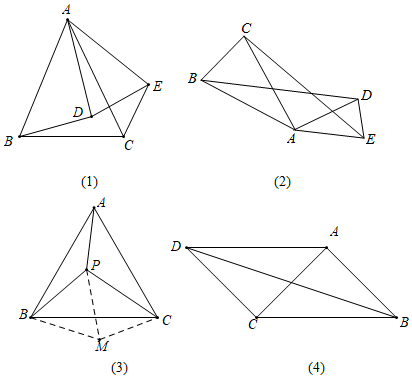
（1）熟悉模型：如圖（2），已知△ABC與△ADE都是等腰三角形，AB=AC，AD=AE，且∠BAC=∠DAE，求證：BD=CE；
（2）運用模型：如圖（3），P為等邊△ABC內一點，且PA：PB：PC=3：4：5，求∠APB的度數(shù)．小明在解決此問題時，根據(jù)前面的“手拉手全等模型”，以BP為邊構造等邊△BPM，這樣就有兩個等邊三角形共頂點B，然后連接CM，通過轉化的思想求出了∠APB的度數(shù)，則∠APB的度數(shù)為度；
（3）深化模型：如圖（4），在四邊形ABCD中，AD=4，CD=3，∠ABC=∠ACB=∠ADC=45°，求BD的長．發(fā)布：2025/6/9 14:30:1組卷：2356引用：3難度：0.2 -
2．如圖1．已知正方形ABCD中，BD為對角線，邊長為3．E為邊CD上一點，過E點作EF⊥BD于F點，
EF=2
（1）如圖1．連結CF，求線段CF的長；
（2）保持△DEF不動，將正方形ABCD繞D點旋轉至如圖2的位置，連結BE，M點為BE的中點，連接MC、MF，探求MC與MF關系，并證明你的結論；
（3）保持△DEF不動，將正方形ABCD繞D點旋轉一周，求出BE的中點M在這個過程中的運動路徑長及MC的最小值．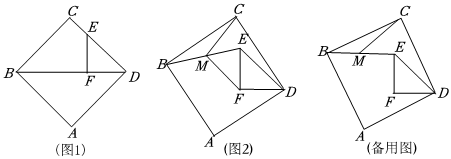
發(fā)布：2025/6/9 14:30:1組卷：559引用：5難度：0.1 -
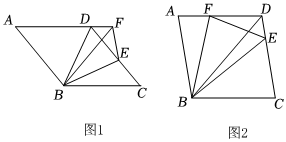3．如圖1，BD是菱形ABCD的對角線，點E是邊CD上一點，將△BCE沿著BE翻折，點C的對應點F恰好落在AD的延長線上，且AB=5．
（1）求證：FB平分∠AFE；
（2）如圖2，若點F落在AD上．
①猜想∠ABF與∠DBE之間的數(shù)量關系，并證明你的結論；
②若，求證：EC=3DE．DFFB=23發(fā)布：2025/6/9 14:30:1組卷：155引用：3難度：0.3