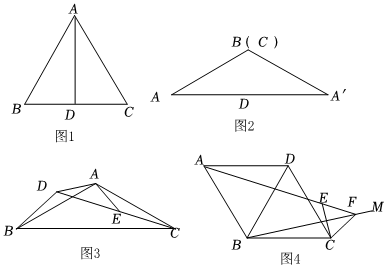
問題背景：如圖1，在等邊△ABC中，作AD⊥BC于點D，則D為BC的中點，∠BAD=∠CAD=12∠BAC=30°，設BD=a,則CD=a,AB=BC=AC=2a,由勾股定理可知AD=3a．若將△ABD和△ACD重新組合為如圖2的△ABA'，此時，∠ABA'=120°，AB=A'B，我們可以得到AA′AB=2ADAB=3．請運用此結論完成以下任務．
遷移應用：如圖3，AB=AC，AD=AE，∠BAC=∠DAE=120°，D、E、C三點在同一條直線上，連接BD．
（1）求證：△ADB≌△AEC．
（2）請直接寫出線段AD、BD、CD之間的數量關系．
（3）如圖4，△ABD與△CBD都是等邊三角形，在∠ABC內作射線BM，作點C關于BM的對稱點E，連接AE并延長交BM于點F，連接CE、CF．若AE=5，EF=2，求BF的長．
1
2
∠
BAC
=
30
°
AD
=
3
a
AA
′
AB
=
2
AD
AB
=
3
【考點】三角形綜合題．
【答案】（1）見解析過程；
（2）CD=AD+BD；
（3）3．
（2）CD=
3
（3）3
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/20 4:0:1組卷：272引用：3難度：0.3
相似題
-
1．已知在平面直角坐標系中，點A（a,b）滿足
=0，AB⊥x軸于點B．12a-3+（2-b）2
（1）點A的坐標為，點B的坐標為；
（2）如圖1，若點M在x軸上，連接MA，使S△ABM=2，求出點M的坐標；
（3）如圖2，P是線段AB所在直線上一動點，連接OP，OE平分∠PON，交直線AB于點E，作OF⊥OE，當點P在直線AB上運動過程中，請探究∠OPE與∠FOP的數量關系，并證明．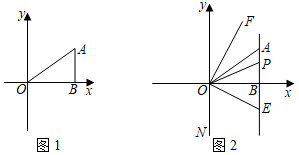
發布：2025/6/7 7:0:1組卷：642引用：7難度：0.3 -
2．如圖，以直角三角形AOC的直角頂點O為原點，以OC，OA所在直線為軸和軸建立平面直角坐標系，點A（0，a），C（b,0）滿足
+|b-8|=0．a-6
（1）a=；b=．
（2）已知坐標軸上有兩動點P，Q同時出發，P點從C點出發以每秒2個單位長度的速度向點O勻速移動，Q點從O點出發以每秒1個單位長度的速度向點A勻速移動，點P到達O點整個運動隨之結束．AC的中點D的坐標是（4，3），設運動時間為t秒．
問：是否存在這樣的t,使得△ODP與△ODQ的面積相等？若存在，請求出t的值；若不存在，請說明理由．
（3）在（2）的條件下，若∠DOC=∠DCO，點G是第二象限中一點，并且y軸平分∠GOD．點E是線段OA上一動點，連接CE交OD于點H，當點E在線段OA上運動的過程中，探究∠GOD，∠OHC，∠ACE之間的數量關系，并證明你的結論．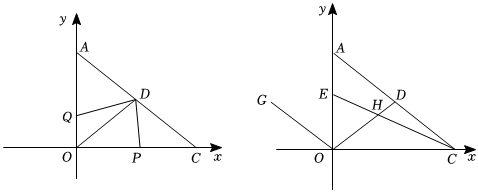
發布：2025/6/7 7:30:1組卷：146引用：1難度：0.1 -
3．如圖1，在△ABC中，BO⊥AC于點O，AO=BO=3，OC=1，過點A作AH⊥BC于點H，交BO于點P．
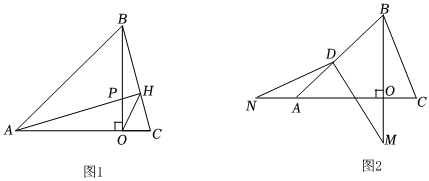
（1）求線段OP的長度；
（2）連接OH，求∠AHO的度數；
（3）如圖2，若點D為AB的中點，點M為線段BO延長線上一動點，連接MD，過點D作DN⊥DM交線段OA延長線于N點，則S△BDM-S△ADN的值是否發生改變，如改變，求出該值的變化范圍；若不改變，求該式子的值．發布：2025/6/7 5:30:3組卷：341引用：3難度：0.1