已知,AB∥CD,F、G分別為直線AB、CD上的點,E為平面內任意一點,連接EF、EG.
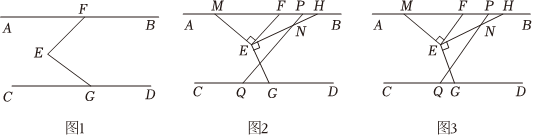
(1)如圖1,請直接寫出∠AFE、∠CGE與∠FEG之間的數量關系.
(2)如圖2,過點E作EM⊥EF、EH⊥EG交直線AB上的點M、H,點N在EH上,過N作PQ∥EF,求證:∠HNQ=∠MEG.
(3)如圖3,在(2)的條件下,若∠ENQ=∠EMF,∠EGD=110°,求∠CQP的度數.
【答案】(1)∠AFE+∠CGE=∠FEN;
(2)見解析;
(3)125°.
(2)見解析;
(3)125°.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/8/23 6:0:3組卷:83引用:2難度:0.7
相似題
-
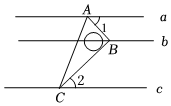 1.如圖所示,直線a∥b∥c,有一塊直角三角板ABC(∠ABC=90°)的三個頂點剛好落在三條直線上,若∠1=50°,則∠2的度數是( )
1.如圖所示,直線a∥b∥c,有一塊直角三角板ABC(∠ABC=90°)的三個頂點剛好落在三條直線上,若∠1=50°,則∠2的度數是( )A.40° B.45° C.50° D.60° 發布:2025/5/25 20:0:1組卷:469引用:4難度:0.8 -
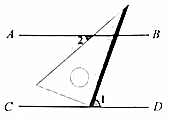 2.一只含有30°的三角板如圖放置,已知AB∥CD,∠1=70°,則∠2=°.發布:2025/5/25 20:0:1組卷:133引用:2難度:0.6
2.一只含有30°的三角板如圖放置,已知AB∥CD,∠1=70°,則∠2=°.發布:2025/5/25 20:0:1組卷:133引用:2難度:0.6 -
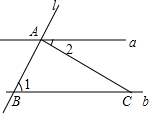 3.如圖,直線a∥b,直線l與直線a、b分別相交于A、B兩點,過點A作直線l的垂線交直線b于點C,若∠2=40°,則∠1的度數為( )
3.如圖,直線a∥b,直線l與直線a、b分別相交于A、B兩點,過點A作直線l的垂線交直線b于點C,若∠2=40°,則∠1的度數為( )A.20° B.30° C.40° D.50° 發布:2025/5/25 20:30:1組卷:256引用:3難度:0.8


