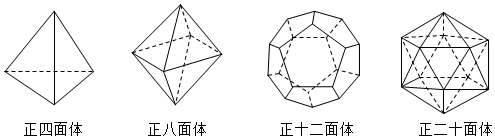
設P為多面體M的一個頂點，定義多面體M在P處的離散曲率為
1
-
1
2
π
（
∠
Q
1
P
Q
2
+
∠
Q
2
P
Q
3
+
?
+
∠
Q
k
P
Q
1
）
，其中Q_i（i=1，2，3，?，k≥3）為多面體M的所有與點P相鄰的頂點，且平面Q₁PQ₃，Q₂PQ₃，?，Q_kPQ₁遍及多面體M的所有以P為公共點的面．如圖是正四面體、正八面體、正十二面體和正二十面體，若它們在各頂點處的離散曲率分別是a,b,c,d,則a,b,c,d的大小關系是（　　）

A．a＞b＞c＞d

B．a＞b＞d＞c

C．b＞a＞d＞c

D．c＞d＞b＞a

【答案】B

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/5/4 8:0:8組卷：88引用：2難度：0.6

相似題

1．一個棱錐的各條棱都相等，那么這個棱錐必不是（　　）
A．三棱錐 B．四棱錐 C．五棱錐 D．六棱錐
發布：2024/12/19 6:30:1組卷：853引用：14難度：0.9
解析
2．已知四棱錐S-ABCD的底面為矩形，SA⊥底面ABCD，點E在線段BC上，以AD為直徑的圓過點E．若SA=
3
AB=3，則△SED的面積的最小值為（　　）
A．9 B．7 C．
9
2
D．
7
2
發布：2024/11/18 2:0:1組卷：181引用：5難度：0.5
解析
3．如圖所示的四個幾何體，其中判斷正確的是（　　）
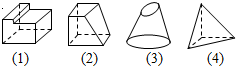
A．（1）不是棱柱 B．（2）是棱柱
C．（3）是圓臺 D．（4）是棱錐
發布：2024/9/30 5:0:1組卷：135引用：2難度：0.9
解析

相關試卷

A．（1）不是棱柱	B．（2）是棱柱
C．（3）是圓臺	D．（4）是棱錐

1．一個棱錐的各條棱都相等，那么這個棱錐必不是（ ）