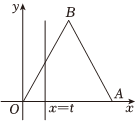
 如圖,△OAB是邊長為2的正三角形,記△OAB位于直線x=t(t>0)左側(cè)的圖形的面積為f(t).
如圖,△OAB是邊長為2的正三角形,記△OAB位于直線x=t(t>0)左側(cè)的圖形的面積為f(t).
(1)求函數(shù)f(t)解析式;
(2)若t0∈(0,2]時,f(t0)=3成立,則當(dāng)正實數(shù)b滿足2a+2b=t0時,求ba+1b的最小值.
f
(
t
0
)
=
3
b
a
+
1
b
【答案】(1)
;(2)3.
f
(
t
)
=
3 2 t 2 , | 0 < t ≤ 1 |
- 3 2 ( t 2 - 4 t + 2 ) , | 1 < t ≤ 2 |
3 , | t ≥ 2 |
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/10/12 7:0:1組卷:21引用:1難度:0.5
相似題
-
1.已知函數(shù)f(x)的圖象如圖所示,則該函數(shù)的解析式為( )
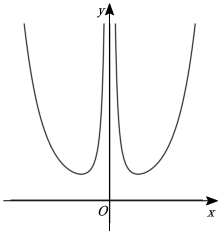
A. f(x)=x2ex+e-xB. f(x)=ex+e-xx2C. f(x)=x2ex-e-xD. f(x)=ex-e-xx2發(fā)布:2024/12/2 8:0:27組卷:102引用:5難度:0.7 -
2.已知f(x+1)=2x+1,則f(2)=( )
A.2 B.5 C.3 D.-3 發(fā)布:2024/12/21 4:30:3組卷:50引用:2難度:0.8 -
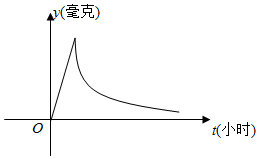 3.為了預(yù)防流感,某學(xué)校對教室用藥熏消毒法進行消毒,已知藥物釋放過程中,室內(nèi)每立方米空氣中含藥量y(毫克)與時間t(小時)成正比.已知6分鐘后藥物釋放完畢,藥物釋放完畢后,y與t的函數(shù)關(guān)系是為y=()116,如圖所示,根據(jù)圖中提供的信息,回答下列問題:t-110
3.為了預(yù)防流感,某學(xué)校對教室用藥熏消毒法進行消毒,已知藥物釋放過程中,室內(nèi)每立方米空氣中含藥量y(毫克)與時間t(小時)成正比.已知6分鐘后藥物釋放完畢,藥物釋放完畢后,y與t的函數(shù)關(guān)系是為y=()116,如圖所示,根據(jù)圖中提供的信息,回答下列問題:t-110
(1)求從藥物釋放開始,每立方米空氣中的含藥量y(毫克)與時間t(小時)之間的函數(shù)關(guān)系式;
(2)據(jù)測定,當(dāng)空氣中每立方米的含藥量降低到0.125毫克以下時,學(xué)生方可進教室,那么從藥物釋放開始,至少需要經(jīng)過多少分鐘后,學(xué)生才能回到教室?發(fā)布:2024/12/3 8:0:1組卷:51引用:1難度:0.5


