數學教育家波利亞曾說：“對一個數學問題，改變它的形式，變換它的結構，直到發現有價值的東西，這是數學解題的一個重要原則”．在復習二次根式時，老師提出了一個求代數式最小值的問題，如：“當0＜x＜12時，求代數式x2+4+（12-x）2+9的最小值”，其中x2+4可看作兩直角邊分別為x和2的Rt△ACP的斜邊長，（12-x）2+9可看作兩直角邊分別是12-x和3的Rt△BDP的斜邊長．于是構造出如圖，將問題轉化為求AP+BP的最小值，運用此方法，請你解決問題：已知x,y均為正數，且x-6=-y.則x2+9+y2+25的最小值是（ ）
x
2
+
4
+
（
12
-
x
）
2
+
9
x
2
+
4
（
12
-
x
）
2
+
9
x
2
+
9
+
y
2
+
25
【考點】軸對稱-最短路線問題；勾股定理．
【答案】C
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/4 5:30:2組卷：519引用：8難度：0.8
相似題
-
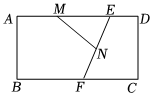1．如圖，矩形ABCD的邊AB=2，BC=4，E是AD上一點，DE=1，F是BC上一動點，M、N分別是AE、EF的中點，則MN+EN的最小值是 ．發布：2025/6/5 23:0:2組卷：432引用：5難度：0.5 -
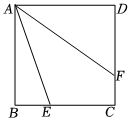2．如圖，正方形ABCD中，AB=3，動點E、F分別在邊BC、CD上，且保持BE=CF．
（1）若BE=CF=1，則AE+AF=；
（2）AE+AF的最小值為 ．發布：2025/6/5 23:30:2組卷：101引用：1難度：0.5 -
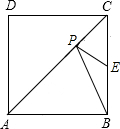3．如圖，正方形ABCD中，AB=4，E是BC的中點，點P是對角線AC上一動點，則PE+PB的最小值為 ．發布：2025/6/6 4:0:1組卷：1273引用：32難度：0.5