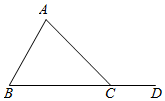
如圖，D是△ABC的AC邊上一點，∠A=∠ABD，∠BDC=150°，∠ABC=85°．
求：（1）∠A的度數；
（2）∠C的度數．
解（1）∵∠BDC是△ABD的外角，∠BDC=150°（已知），
∴∠BDC=∠A∠A+∠ABD∠ABD（ 三角形的一個外角等于與它不相鄰的兩個內角的和三角形的一個外角等于與它不相鄰的兩個內角的和）．
又∵∠A=∠ABD（已知），
∴∠A=7575度．（等量代換）．
（2）∵∠A+∠ABC+∠C=180180度（ 三角形的內角和等于180°三角形的內角和等于180°），
∴∠C=180°-∠ABC-∠A（等式性質）．
又∵∠ABC=85°，
∴∠C=2020度．
【考點】三角形的外角性質．
【答案】∠A；∠ABD；三角形的一個外角等于與它不相鄰的兩個內角的和；75；180；三角形的內角和等于180°；20
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：344引用：2難度：0.6
相似題
-
1．將一副三角板按如圖所示放置，使含30°角的三角板的斜邊與含45°角三角板的直角邊在一條直線上．則∠1的度數是（ ）發布：2025/6/9 1:30:1組卷：131引用：3難度：0.6 -
2．如圖，△ABC中，∠ABC的平分線BD與外角∠ACE的平分線CD相交于點D，若∠D=25°，則∠A的度數為（ ）發布：2025/6/9 2:0:7組卷：318引用：1難度：0.5 -
3．定理：三角形的一個外角等于與它不相鄰的兩個內角的和．
已知：如圖，∠ACD是△ABC的外角．求證：∠ACD=∠A+∠B．
下列說法正確的是（ ）證法1：如圖，
∵∠A+∠B+∠ACB=180°（三角形內角和定理），
又∵∠ACD+∠ACB=180°（平角定義），
∴∠ACD+∠ACB=∠A+∠B+∠ACB（等量代換）．
∴∠ACD=∠A+∠B（等式性質）．證法2：如圖，
∵∠A=76°，∠B=59°，
且∠ACD=135°（量角器測量所得）
又∵135°=76°+59°（計算所得）
∴∠ACD=∠A+∠B（等量代換）．發布：2025/6/9 1:30:1組卷：1359引用：23難度：0.7