“關(guān)聯(lián)”是解決數(shù)學(xué)問題的重要思維方式．角平分線的有關(guān)聯(lián)想就有很多……
【問題提出】
（1）如圖①，PC是△PAB的角平分線，求證PAPB=ACBC．
PA
PB
AC
BC
| 小明思路：關(guān)聯(lián)“平行線、等腰三角形”，利用“三角形相似”． 小紅思路：關(guān)聯(lián)“角平分線上的點(diǎn)到角的兩邊的距離相等”，利用“等面積法”． |
【作圖應(yīng)用】
（2）如圖②，AB是⊙O的弦，在⊙O上作出點(diǎn)P，使得
PA
PB
要求：（1）用直尺和圓規(guī)作圖；（2）保留作圖的痕跡，寫出必要的文字說明．
【深度思考】
（3）如圖③，PC是△PAB的角平分線，若AC=3，BC=1，則△PAB的面積最大值是
3
3
．【考點(diǎn)】圓的綜合題．
【答案】3
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：1379引用：2難度：0.1
相似題
-
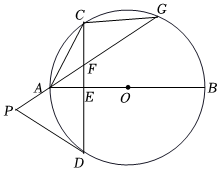1．如圖，AB為⊙O的直徑，弦CD⊥AB于點(diǎn)E，F(xiàn)是CD上一點(diǎn)，且AF=CF，點(diǎn)P在FA的延長線上，且∠PFD=∠PDF，延長PF與⊙O交于點(diǎn)G，連接AC，CG．
（1）求證：△AFC∽△ACG；
（2）求證：PD是⊙O的切線；
（3）若tanG=，BE-AE=34，求73的值．S△AFCS△CFG發(fā)布：2025/5/24 5:30:2組卷：72引用：1難度：0.4 -
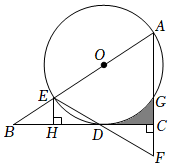2．如圖，在△AEF中，∠F=∠AEF，以AE為直徑作⊙O，分別交邊AF和邊EF于點(diǎn)G和點(diǎn)D，過點(diǎn)D作DC⊥AF交AF于點(diǎn)C，延長CD交AE的延長線于點(diǎn)B，過點(diǎn)E作EH⊥BC于點(diǎn)H．
（1）試判斷BD與⊙O的位置關(guān)系，并說明理由；
（2）證明：EH=CF．
（3）若∠B=30°，AE=12，求圖中陰影部分的面積．發(fā)布：2025/5/24 6:0:2組卷：164引用：5難度：0.2 -
3．如圖，四邊形ABCD內(nèi)接于⊙O，AC是⊙O的直徑，AB=BC，延長DA到點(diǎn)E，使得BE=BD．
（1）若AF平分∠CAD，求證：BA=BF；
（2）試探究線段AD，CD與BD之間的數(shù)量關(guān)系．發(fā)布：2025/5/24 5:0:1組卷：169引用：1難度：0.4