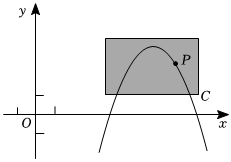
如圖，點P（a,3）在拋物線C：y=4-（6-x）²上，且在C的對稱軸右側．
（1）寫出C的對稱軸和y的最大值；
（2）求a的值，并求出點P到對稱軸的距離；
（3）坐標平面上放置一透明膠片，并在膠片上描畫出點P及C的一段，分別記為P'，C'．平移該膠片，使C'所在拋物線對應的函數恰為y=-x²+4x-4．求點P'移動的最短路程．

【答案】（1）直線x=6，y的最大值為4；
（2）a=7；點P到對稱軸的距離為1；
（3）P'移動的最短路程為4

．

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/5/31 14:30:1組卷：143引用：2難度：0.6

相似題

1．二次函數y=x²-4x+1圖象的對稱軸是直線

．
發布：2025/6/2 0:0:1組卷：157引用：4難度：0.7
解析
2．拋物線y=（x-1）²+3的頂點坐標是（　　）
A．（1，3） B．（-1，3） C．（1，-3） D．（3，-1）
發布：2025/6/1 22:30:2組卷：631引用：16難度：0.9
解析
3．對于實數c、d,我們可用min{c,d}表示c、d兩數中較小的數，如min{3，-1}=-1．若關于x的函數y=min{2x²，a（x-t）²}的圖象關于直線x=3對稱，則a、t的值可能是（　　）
A．3，6 B．2，-6 C．2，6 D．-2，6
發布：2025/6/1 23:0:1組卷：46引用：1難度：0.6
解析

相關試卷

1．二次函數y=x2-4x+1圖象的對稱軸是直線 ．