十五世紀杰出的法國數學家尼古拉斯?丘凱（Nicolas chuquet）在他的名著《數學三章》中提到了“平均數的規則”即：已知a、b、c、d都是正整數，如果

a

b

＜

c

d

，那么

a

b

＜

a

+

c

b

+

d

＜

c

d

，并給出了證明．
（1）根據我們所學習過的不等式的性質，我們不難證明這個結論．
由

a

b

＜

c

d

，在不等式的兩邊同時乘以

bd

bd

，可以得到ad＜bc；
由ad＜bc,在不等式的兩邊同時加上

ab

ab

，可以得到ad+ab＜bc+ab；
由ad+ab＜bc+ab,在不等式的兩邊同時除以

b（b+d）

b（b+d）

，可以得到

a

b

＜

a

+

c

b

+

d

；
同理可證

a

+

c

b

+

d

＜

c

d

，所以

a

b

＜

a

+

c

b

+

d

＜

c

d

成立．
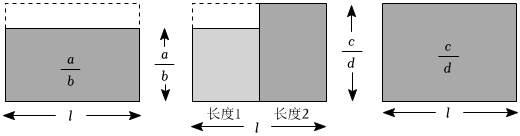
（2）丘凱在《數學三章》中對于“平均數的規則“給出了兩種證明，其中一種是用圖形幾何的方式直觀地說明了“平均數的規則”成立．
長度1是

abd

-

b

2

c

abd

-

b

2

c

+

a

d

2

-

bcd

abd

-

b

2

c

abd

-

b

2

c

+

a

d

2

-

bcd

；長度2是

l-

abd

-

b

2

c

abd

-

b

2

c

+

a

d

2

-

bcd

l-

abd

-

b

2

c

abd

-

b

2

c

+

a

d

2

-

bcd

．（用含有字母的式子表示）