蜂房是自然界最神奇的“建筑”之一，如圖1所示．蜂房結構是由正六棱柱截去三個相等的三棱錐H-ABC，J-CDE，K-EFA，再分別以AC，CE，EA為軸將△ACH，△CEJ，△EAK分別向上翻轉180°，使H，J，K三點重合為點S所圍成的曲頂多面體（下底面開口），如圖2所示．蜂房曲頂空間的彎曲度可用曲率來刻畫，定義其度量值等于蜂房頂端三個菱形的各個頂點的曲率之和，而每一頂點的曲率規定等于2π減去蜂房多面體在該點的各個面角之和（多面體的面角是多面體的面的內角，用弧度制表示）．例如：正四面體在每個頂點有3個面角，每個面角是π3，所以正四面體在各頂點的曲率為2π-3×π3=π．
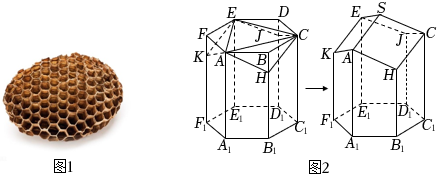
（1）求蜂房曲頂空間的彎曲度；
（2）若正六棱柱底面邊長為1，側棱長為2，設BH=x
（i）用x表示蜂房（圖2右側多面體）的表面積S（x）；
（ii）當蜂房表面積最小時，求其頂點S的曲率的余弦值．
π
3
2
π
-
3
×
π
3
=
π
【考點】棱柱、棱錐、棱臺的側面積和表面積．
【答案】（1）2π；
（2）（i）；
（ii）．
（2）（i）
S
（
x
）
=
3
3
?
2
?
1
+
4
x
2
?
-
3
x
+
12
+
3
3
?
2
，
x
∈
（
0
，
2
）
（ii）
23
27
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/9 9:0:1組卷：153引用：5難度：0.4