如圖，在某中學的一場籃球賽中，李明在距離籃圈中心5.5m（水平距離）處跳起投籃，球出手時離地面2.2m,當籃球運行的水平距離為3m時達到離地面的最大高度4m.已知籃球在空中的運行路線為一條拋物線，籃圈中心距地面3.05m.
（1）建立如圖所示的平面直角坐標系，求籃球運動路線所在拋物線的函數解析式；
（2）場邊看球的小麗認為，李明投出的此球不能命中籃圈中心．請通過計算說明小麗判斷的正確性；
（3）在球出手后，未達到最高點時，被防守隊員攔截下來稱為蓋帽．但球到達最高點后，處于下落過程時，防守隊員再出手攔截，屬于犯規．在（1）的條件下，防守方球員張亮前來蓋帽，已知張亮的最大摸球高度為3.2m,則他應該在李明前面多少米范圍內跳起攔截才能蓋帽成功？
【考點】二次函數的應用．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1594引用：8難度：0.6
相似題
-
1．如圖，某隧道口的橫截面是拋物線形，已知路寬AB為6米，最高點離地面的距離OC為5米．以最高點O為坐標原點，拋物線的對稱軸為y軸，1米為數軸的單位長度，建立平面直角坐標系，
求：（1）以這一部分拋物線為圖象的函數解析式，并寫出x的取值范圍；
（2）有一輛寬2.8米，高1米的農用貨車（貨物最高處與地面AB的距離）能否通過此隧道？發布：2025/5/28 6:0:2組卷：1005引用：17難度：0.1 -
2．周長是4m的矩形，它的面積S（m2）與一邊長x（m）的函數圖象大致是（ ）
發布：2025/5/28 4:30:1組卷：1057引用：5難度：0.5 -
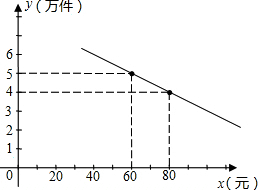3．某通訊器材公司銷售一種市場需求較大的新型通訊產品．已知每件產品的進價為40元，每年銷售該種產品的總開支（不含進價）總計120萬元．在銷售過程中發現，年銷售量y（萬件）與銷售單價x（元）之間存在著如圖所示的一次函數關系．
（1）求y關于x的函數關系式；
（2）試寫出該公司銷售該種產品的年獲利z（萬元）關于銷售單價x（元）的函數關系式（年獲利=年銷售額一年銷售產品總進價一年總開支）．當銷售單價x為何值時，年獲利最大并求這個最大值；
（3）若公司希望該種產品一年的銷售獲利不低于40萬元，借助（2）中函數的圖象，請你幫助該公司確定銷售單價的范圍．在此情況下，要使產品銷售量最大，你認為銷售單價應定為多少元？發布：2025/5/28 3:0:1組卷：416引用：44難度：0.1
相關試卷