定義：長寬比為n：1（n為正整數）的矩形稱為n矩形．
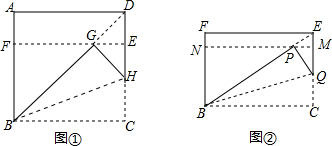
下面，我們通過折疊的方式折出一個2矩形，如圖①所示．
操作1：將正方形ABCD沿過點B的直線折疊，使折疊后的點C落在對角線BD上的點G處，折痕為BH．
操作2：將AD沿過點G的直線折疊，使點A，點D分別落在邊AB，CD上，折痕為EF．
則四邊形BCEF為2矩形．
證明：設正方形ABCD的邊長為1，則BD=12+12=2．
由折疊性質可知BG=BC=1，∠AFE=∠BFE=90°，則四邊形BCEF為矩形．
∴∠A=∠BFE．
∴EF∥AD．
∴BGBD=BFAB，即12=BF1．
∴BF=12．
∴BC：BF=1：12=2：1．
∴四邊形BCEF為2矩形．
閱讀以上內容，回答下列問題：
（1）在圖①中，所有與CH相等的線段是 GH、DGGH、DG，tan∠HBC的值是 2-12-1；
（2）已知四邊形BCEF為2矩形，模仿上述操作，得到四邊形BCMN，如圖②，求證：四邊形BCMN是3矩形；
（3）將圖②中的3矩形BCMN沿用（2）中的方式操作3次后，得到一個“n矩形”，則n的值是 66．
n
n
2
2
1
2
+
1
2
2
BG
BD
BF
AB
1
2
BF
1
1
2
1
2
2
2
2
2
2
3
3
n
【答案】GH、DG；-1；6
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1273引用：10難度：0.1
相似題
-
1．閱讀下面的材料，并解決問題：
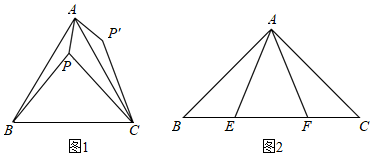
（1）如圖1，等邊△ABC內有一點P，若點P到頂點A、B、C的距離分別是3、4、5，求∠APB的度數．由于PA、PB、PC不在一個三角形中，為了解決本題我們可以將△ABP繞頂點A旋轉到△ACP′處，此時△ACP≌．這樣，就可以利用全等三角形知識，將三條線段的長度轉化到一個三角形中從而求出∠APB的度數；（求∠APB的度數）
（2）請你利用第（1）題解答的思想方法，解答下面的問題：如圖2，在△ABC中，∠CAB=90°，AB=AC，E、F為BC上的點且∠EAF=45°，求證：EF2=BE2+FC2．發布：2025/6/9 5:30:2組卷：189引用：2難度：0.2 -
2．如圖1，在△ABC中，AE⊥BC于點E，AE=BE，D是AE上的一點，且DE=CE，連接BD，CD．
（1）試判斷BD與AC的位置關系是：；數量關系是：；
（2）如圖2，若將△DCE繞點E旋轉一定的角度后，試判斷BD與AC的位置關系和數量關系是否發生變化，并說明理由；
（3）如圖3，若將（2）中的等腰直角三角形都換成等邊三角形，其他條件不變．
①試猜想BD與AC的數量關系為：；
②你能求出BD與AC的夾角度數嗎？如果能，請直接寫出夾角度數；如果不能，請說明理由．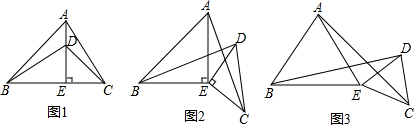
發布：2025/6/9 6:30:1組卷：724引用：2難度：0.3 -
3．在Rt△ABC中，∠ACB=90°，AC=3，BC=4．將Rt△ABC繞點B順時針旋轉α（0°＜α＜60°）得到Rt△DEB，直線DE，AC交于點P．
（1）如圖1，當BD⊥BC時，連接BP．
①求△BDP的面積；
②求tan∠CBP的值；
（2）如圖2，連接AD，若F為AD中點，求證：C，E，F三點共線．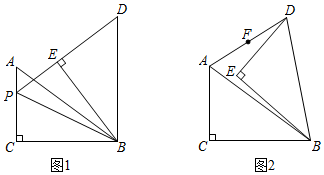
發布：2025/6/9 17:0:1組卷：511引用：4難度：0.1