在矩形ABCD中，AB=3，AD=5，E是射線DC上的點，連接AE，將△ADE沿直線AE翻折得△AFE．
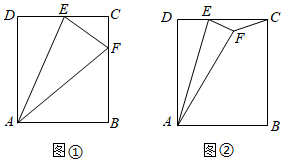
（1）如圖①，點F恰好在BC上，求證：△ABF∽△FCE：
（2）如圖②，點F在矩形ABCD內，連接CF，若DE=1，求△EFC的面積；
（3）若以點E，F，C為頂點的三角形是直角三角形，請直接寫出DE的長．
【考點】相似形綜合題．
【答案】（1）證明過程見解析；
（2）；
（3）或或5或15．
（2）
5
13
（3）
5
（
√
34
-
5
）
3
5
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/23 18:0:1組卷：375引用：4難度：0.4
相似題
-
1．在矩形ABCD中，AD=3，CD=4，點E在邊CD上，且DE=1．
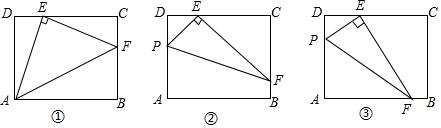
感知：如圖①，連接AE，過點E作EF⊥AE，交BC于點F，連接AF，易證：△ADE≌△ECF（不需要證明）；
探究：如圖②，點P在矩形ABCD的邊AD上（點P不與點A、D重合），連接PE，過點E作EF⊥PE，交BC于點F，連接PF．求證：△PDE∽△ECF；
應用：如圖③，若EF交AB邊于點F，其他條件不變，且△PEF的面積是3，則AP的長為．發布：2025/6/16 19:30:1組卷：681引用：3難度：0.1 -
2．如圖，已知直線l1∥l2，線段AB在直線l1上，BC垂直于l1交l2于點C，且AB=BC，P是線段BC上異于兩端點的一點，過點P的直線分別交l2、l1于點D、E（點A、E位于點B的兩側），滿足BP=BE，連接AP、CE．
（1）求證：△ABP≌△CBE；
（2）連接AD、BD，BD與AP相交于點F．如圖2．
①當=2時，求證：AP⊥BD；BCBP
②當=n（n＞1）時，設△PAD的面積為S1，△PCE的面積為S2，求BCBP的值．S1S2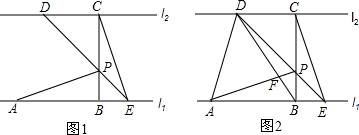
發布：2025/6/18 11:30:2組卷：1185引用：6難度：0.3 -
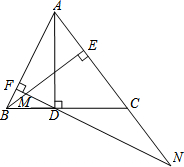3．如圖，AD、BE是△ABC的兩條高，過點D作DF⊥AB，垂足為F，FD交BE于M，FD、AC的延長線交于點N．
（1）求證：△BFM∽△NFA；
（2）試探究線段FM、DF、FN之間的數量關系，并證明你的結論；
（3）若AC=BC，DN=12，ME：EN=1：2，求線段AC的長．發布：2025/6/16 11:30:2組卷：851引用：7難度：0.3