如圖，在Rt△ABC中，∠C=90°，∠BAC=60°，AB=8，半徑為3的⊙M與射線BA相切，切點為N，且AN=3，將Rt△ABC繞點A順時針旋轉，設旋轉角為α（0°≤α≤180°）
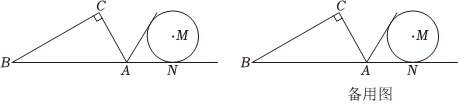
（1）AC的長為 44；
（2）求當旋轉角α為多少時，AC與⊙M相切；
（3）當AC落在AN上時，設點B，C的對應點分別是點D，E．
①畫出旋轉后AC落在射線AN上時的Rt△ADE（草圖即可），此時Rt△ADE的斜邊AD所在的直線與⊙M的位置關系是 相切相切；
②求出Rt△ADE的直角邊DE被⊙M截得的弦PQ的長．
3
【考點】圓的綜合題．
【答案】4；相切
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/8 8:0:8組卷：193引用：2難度：0.1
相似題
-
1．如圖，已知四邊形ABCD內接于⊙O，連接AC、BD，∠ADC+2∠ACD=180°．
（1）求證：BD平分∠ABC；
（2）如圖2，若∠ADB+∠BAC=90°，求證：AB=AC．12
（3）在（2）的條件下，連接DO并延長交⊙O于點E，交AB、AC于點H、K，連接EB，當AC=30，BE=11時，求tan∠ABC的值．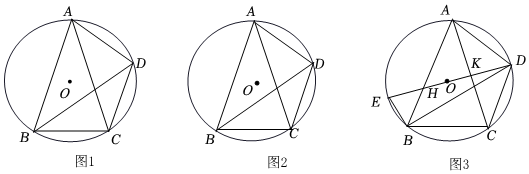
發布：2025/5/25 15:0:2組卷：245引用：1難度：0.3 -
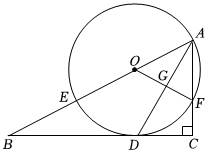2．如圖，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于點D，O為AB上一點，經過點A，D的⊙O分別交AB，AC于點E、F，連接OF交AD于點G．
（1）求證：BC是⊙O的切線；
（2）求證：AD2=AB?AF；
（3）若BE=8，tanB=，求AD的長．512發布：2025/5/25 14:0:1組卷：308引用：1難度：0.3 -
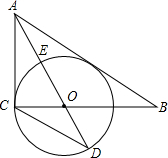3．如圖，在Rt△ABC中，∠ACB=90°，AO是△ABC的角平分線．以O為圓心，OC為半徑作⊙O．
（1）求證：AB是⊙O的切線．
（2）已知AO交⊙O于點E，延長AO交⊙O于點D，tanD=，求12的值．AEAC
（3）在（2）的條件下，設⊙O的半徑為3，求AB的長．發布：2025/5/25 13:30:1組卷：5031引用：18難度：0.1