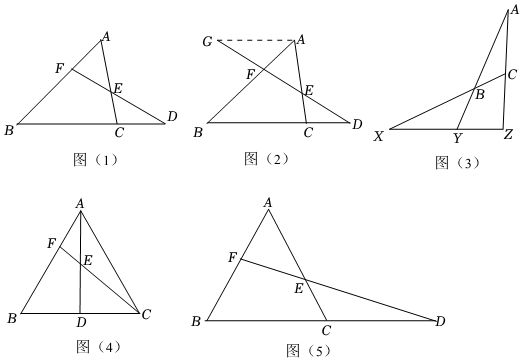
梅涅勞斯（Menelaus）是古希臘數學家，他首先證明了梅涅勞斯定理，定理的內容是：如圖（1），如果一條直線與△ABC的三邊AB，BC，CA或它們的延長線交于F、D、E三點，那么一定有 AFFB?BDDC?CEEA=1．
下面是利用相似三角形的有關知識證明該定理的部分過程：
證明：如圖（2），過點A作AG∥BC，交DF的延長線于點G，則有AFFB=AGBD，CEEA=CDAG，
∴AFFB?BDDC?CEEA=AGBD?BDDC?CDAG=1．
請用上述定理的證明方法解決以下問題：
（1）如圖（3），△ABC三邊CB，AB，AC的延長線分別交直線l于X，Y，Z三點，證明：BXXC?CZZA?AYYB=1，請用上述定理的證明方法或結論解決以下問題：
（2）如圖（4），等邊△ABC的邊長為3，點D為BC的中點，點F在AB上，且BF=2AF，CF與AD交于點E，試求AE的長．
（3）如圖（5），△ABC的面積為4，F為AB中點，延長BC至D，使CD=BC，連接FD交AC于E，求四邊形BCEF的面積．
AF
FB
?
BD
DC
?
CE
EA
AF
FB
=
AG
BD
CE
EA
=
CD
AG
AF
FB
?
BD
DC
?
CE
EA
=
AG
BD
?
BD
DC
?
CD
AG
BX
XC
?
CZ
ZA
?
AY
YB
【考點】梅涅勞斯定理與塞瓦定理．
【答案】（1）見解析；
（2）；
（3）．
（2）
3
3
4
（3）
8
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/1 11:0:2組卷：869引用：1難度：0.2
相似題
-
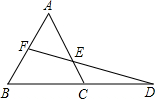1．如圖，等邊△ABC的邊長為2，F為AB中點，延長BC至D，使CD=BC，連接FD交AC于E，則四邊形BCEF的面積為．發布：2025/5/27 7:30:1組卷：1091引用：1難度：0.5 -
2．設A1，B1，C1是直線l1上的任意三點，A2，B2，C2是另一條直線l2上的任意三點，A1B2和B1A2交于L，A1C2和A2C1交于M，B1C2和B2C1交于N．求證：L，M，N三點共線．
發布：2025/5/26 18:0:2組卷：276引用：1難度：0.1 -
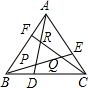3．如圖，D、E、F內分正△ABC的三邊AB、BC、AC均為1：2兩部分，AD、BE、CF相交成的△PQR的面積是△ABC的面積的（ ）發布：2025/5/26 18:0:2組卷：1185引用：3難度：0.9