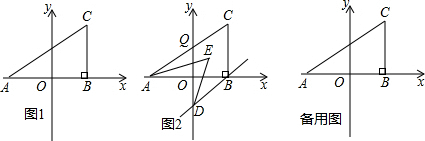
如圖①，在平面直角坐標系中，A（a,0），C（b,4），且滿足（a+4）2+b-4=0，過C作CB⊥x軸于B．
（1）求三角形ABC的面積．
（2）若線段AC與y軸交于點Q（0，2），在y軸上是否存在點P，使得三角形ABC和三角形QCP的面積相等，若存在，求出P點坐標；若不存在，請說明理由．
（3）若過B作BD∥AC交y軸于D，且AE，DE分別平分∠CAB，∠ODB，如圖②，求∠AED的度數(shù)．
b
-
4
【考點】三角形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：321引用：6難度：0.3
相似題
-
1．【問題探究】在學習三角形中線時，我們遇到過這樣的問題：如圖①，在△ABC中，點D為BC邊上的中點，AB=4，AC=6，求線段AD長的取值范圍．我們采用的方法是延長線段AD到點E，使得AD=DE，連結CE，可證△ABD≌△ECD，可得CE=AB=4，根據(jù)三角形三邊關系可求AD的范圍，我們將這樣的方法稱為“三角形倍長中線”．則AD的范圍是：．
【拓展應用】
（1）如圖②，在△ABC中，BC=2BD，AD=3，AC=2，∠BAD=90°，求AB的長．10
（2）如圖③，在△ABC中，D為BC邊的中點，分別以AB、AC為直角邊向外作直角三角形，且滿足∠ABE=∠ACF=30°，連結EF，若AD=2，則EF=．（直接寫出）3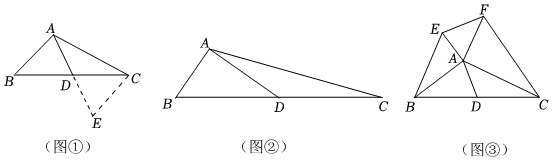
發(fā)布：2025/5/26 8:0:5組卷：411引用：5難度：0.4 -
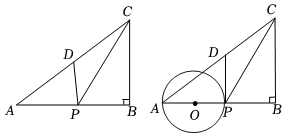2．如圖①，在△ABC中，∠ABC=90°，AC=10，BC=6，D點為AC邊的中點．點P在邊AB上運動（點P不與A、B重合），連結PD、PC．設線段AP的長度為x.
（1）求AB的長．
（2）當△APD是等腰三角形時，求這個等腰三角形的腰長．
（3）連結PD、PC，當PD+PC取最小值時，求x的值．
（4）如圖②，取AP的中點為O，以點O為圓心，以線段AP的長為直徑的圓與線段PD有且只有一個公共點時，直接寫出x的取值范圍．發(fā)布：2025/5/26 6:30:2組卷：176引用：1難度：0.3 -
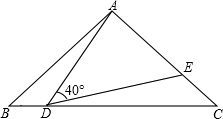3．如圖，在△ABC中，AB=AC=2，∠B=40°，點D在線段BC上運動（D不與B、C重合），連接AD，作∠ADE=40°，DE交線段AC于E．
（1）當∠BDA=115°時，∠BAD=°，∠DEC=°；
（2）當DC等于多少時，△ABD與△DCE全等？請說明理由；
（3）在點D的運動過程中，△ADE的形狀可以是等腰三角形嗎？若可以，請直接寫出∠BDA的度數(shù)．若不可以，請說明理由．發(fā)布：2025/5/26 2:30:2組卷：976引用：8難度：0.3