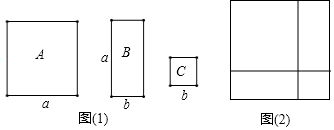
如圖（1），有A、B、C三種不同型號的卡片若干張，其中A型是邊長為a（a＞b）的正方形，B型是長為a、寬為b的長方形，C型是邊長為b的正方形．
（1）若用A型卡片1張，B型卡片2張，C型卡片1張拼成了一個正方形（如圖（2）），此正方形的邊長為
a+b
a+b
，根據該圖形請寫出一條屬于因式分解的等式：
a²+2ab+b²=（a+b）²
a²+2ab+b²=（a+b）²
．
（2）若要拼一個長為2a+b,寬為a+2b的長方形，設需要A類卡片x張，B類卡片y張，C類卡片z張，則x+y+z=
9
9
．
（3）現有A型卡片1張，B型卡片6張，C型卡片11張，從這18張卡片中拿掉兩張卡片，余下的卡片全用上，你能拼出一個長方形或正方形嗎？有幾種拼法？請你通過運算說明理由．

【答案】a+b；a²+2ab+b²=（a+b）²；9

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/7/19 8:0:9組卷：706引用：5難度：0.6

相似題

1．已知a,b,c為△ABC的三條邊的長，
（1）當b²+2ab=c²+2ac時，試判斷△ABC屬于哪一類三角形；
（2）判斷a²-b²-2bc-c²的值的符號，并說明理由．
發布：2025/7/1 13:0:6組卷：207引用：1難度：0.3
解析
2．已知：a＞b＞0，且a²+b²=
10
3
ab,那么
b
+
a
b
-
a
的值為

．
發布：2025/6/25 7:30:2組卷：719引用：4難度：0.9
解析
3．若a²-ab=7-m,b²-ab=9+m,則a-b的值為（　　）
A．2 B．±2 C．4 D．±4
發布：2025/6/25 6:0:1組卷：581引用：2難度：0.7
解析

相關試卷

1．已知a,b,c為△ABC的三條邊的長，（1）當b2+2ab=c2+2ac時，試判斷△ABC屬于哪一類三角形；（2）判斷a2-b2-2bc-c2的值的符號，并說明理由．