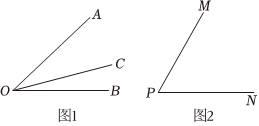
如圖1，射線OC在∠AOB的內部，圖中共有3個角：∠AOB、∠AOC和∠BOC，若其中有一個角的度數(shù)是另一個角度數(shù)的兩倍，則稱射線OC是∠AOB的奇妙線．
（1）一個角的角平分線 是是這個角的奇妙線．（填是或不是）
（2）如圖2，若∠MPN=60°，射線PQ繞點P從PN位置開始，以每秒10°的速度逆時針旋轉，當∠QPN首次等于180°時停止旋轉，設旋轉的時間為t（s）．
①當t為何值時，射線PM是∠QPN的奇妙線？
②若射線PM同時繞點P以每秒6°的速度逆時針旋轉，并與PQ同時停止旋轉．請求出當射線PQ是∠MPN的奇妙線時t的值．
【答案】是
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：11901引用：15難度：0.3
相似題
-
1．如圖，∠AOB=90°，直線CD經(jīng)過點O，∠BOD=110°．
（1）求∠AOC的度數(shù)；
（2）若∠AOE=3∠AOC，試畫出∠AOE，并求出∠EOC的度數(shù)．發(fā)布：2025/6/5 18:30:1組卷：422引用：1難度：0.6 -
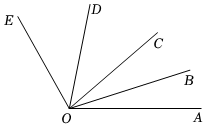2．如圖，OB，OD分別平分∠AOC，∠COE．∠AOE=160°，∠AOB=36°．
求∠AOD的度數(shù)．發(fā)布：2025/6/5 17:30:1組卷：62引用：3難度：0.9 -
3．如圖，以直線AB上一點O為端點作射線OC，使∠BOC=70°，將一個直角三角形的直角頂點放在點O處．（注：∠DOE=90°）
（1）如圖①，若直角三角板DOE的一邊OD放在射線OB上，則∠COE=°；
（2）如圖②，將直角三角板DOE繞點O逆時針方向轉動到某個位置，若OC恰好平分∠BOE，求∠COD的度數(shù)；
（3）如圖③，將直角三角板DOE繞點O轉動，如果OD始終在∠BOC的內部，試猜想∠BOD和∠COE有怎樣的數(shù)量關系？并說明理由．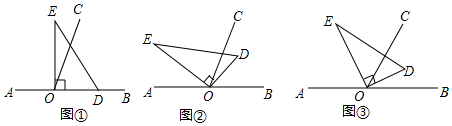
發(fā)布：2025/6/5 15:30:1組卷：5734引用：38難度：0.7