當前位置：
試題詳情
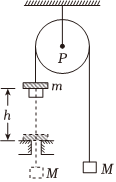如圖所示為著名的“阿特伍德機”裝置示意圖．跨過輕質定滑輪的輕繩兩端懸掛兩個質量質量均為M的物塊，當左側物塊附上質量為m的小物塊時，該物塊由靜止開始加速下落，下落h后小物塊撞擊擋板自動脫離，系統以v勻速運動．忽略系統一切阻力，重力加速度為g,若測出v,則可完成多個力學實驗．下列關于此實驗的說法，正確的是（ ）
【考點】多物體系統的機械能守恒問題；牛頓第二定律的簡單應用．
【答案】B；C
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/11/1 8:0:2組卷：29引用：1難度：0.5
相似題
-
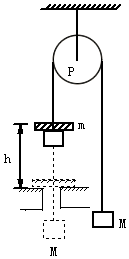1．如圖所示為著名的“阿特伍德機”裝置示意圖，跨過輕質定滑輪的輕繩兩端懸掛兩個質量均為M的物塊，當左側物塊附上質量為m的小物塊時，該物塊由靜止開始加速下落，下落h后小物塊撞擊擋板自動脫離，系統以v勻速運動，忽略系統一切阻力，重力加速度為g,若測出v,則可完成多個力學實驗。下列關于此實驗的說法，正確的是（ ）發布：2024/11/1 8:0:2組卷：42引用：1難度：0.5 -
2．如圖所示，一個表面光滑的斜面體M置于在水平地面上，它的兩個斜面與水平面的夾角分別為α、β，且α＜β，M的頂端裝有一定滑輪，一輕質細繩跨過定滑輪后連接A、B兩個小滑塊，細繩與各自的斜面平行，不計繩與滑輪間的摩擦，A、B恰好在同一高度處于靜止狀態．剪斷細繩后，A、B滑至斜面底端，M始終保持靜止．則（ ）發布：2024/9/22 4:0:8組卷：78引用：2難度：0.9 -
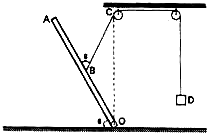3．如圖所示，質量為m、長為L的均勻細桿OA，一端通過光滑鉸鏈固定在地面O處，在細桿中點B處系一根細繩，細繩繞過兩個光滑定滑輪后懸掛著物體D，物體D的質量為細桿質量的1/3，D離滑輪距離足夠遠．在外力F的作用下使細桿與地面保持夾角θ為60°，此時細繩CB與桿的夾角也為60°（如圖所示）．已知細桿繞O點轉動的動能表達式為表示桿的質量，L表示桿的長度，ω表示桿轉動的角速度．求：Ek=16mL2ω2，m
（1）外力F的最小值．
（2）撤去外力F后，細桿從圖示位置到繞O點擺到地面前的過程中，系統（指細桿和物體D）重力勢能的變化量．
（3）撤去外力F后，細桿繞O點轉到地面的瞬間，物體D的速度大小．發布：2024/10/31 8:0:1組卷：57引用：1難度：0.1