當前位置:
試題詳情
我們常利用數形結合思想探索了整式乘法的一些法則和公式.類似地,我們可以借助一個棱長為a的大正方體進行以下探索:
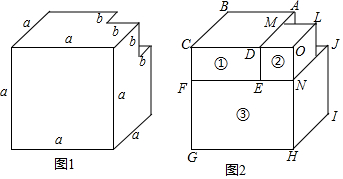
(1)在大正方體一角截去一個棱長為b(b<a)的小正方體,如圖1所示,則得到的幾何體的體積為 a3-b3a3-b3.
(2)將圖1中的幾何體分割成三個長方體①、②、③,如圖2所示,因為BC=a,AB=a-b,CF=b,所以長方體①的體積為ab(a-b),類似地,長方體②的體積為 b2(a-b)b2(a-b),長方體③的體積為 a2(a-b)a2(a-b);(結果不需要化簡)
(3)將表示長方體①、②、③的體積的式子相加,并將得到的多項式分解因式,結果為 (a-b)(a2+ab+b2)(a-b)(a2+ab+b2).
(4)用不同的方法表示圖1中幾何體的體積,可以得到的等式為 a3-b3=(a-b)(a2+ab+b2)a3-b3=(a-b)(a2+ab+b2).
(5)已知a-b=4,ab=2,求a3-b3的值.
【答案】a3-b3;b2(a-b);a2(a-b);(a-b)(a2+ab+b2);a3-b3=(a-b)(a2+ab+b2)
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/12/23 14:0:1組卷:380引用:5難度:0.4


