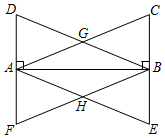
在Rt△ABC與Rt△ABD中，∠ABC=∠BAD=90°，AC=BD，AC、BD相交于點G，過點A作AE∥DB交CB的延長線于點E，過點B作BF∥CA交DA的延長線于點F，AE、BF相交于點H．
（1）證明：△ABD≌△BAC．
（2）證明：四邊形AHBG是菱形．
（3）若AB=BC，證明四邊形AHBG是正方形．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/8/10 3:0:1組卷：287引用：4難度：0.5

相似題

1．在平行四邊形ABCD的對角線AC與BD相交于點O，BC=5，AC=6，BD=8，則四邊形ABCD（　　）
A．平行四邊形 B．矩形 C．菱形 D．正方形
發布：2025/5/22 11:0:1組卷：68引用：2難度：0.6
解析
2．如圖，△ABC中，∠BAC=90°，中線AF與中位線DE相交于點O，則四邊形ADFE是（　　）
A．平行四邊形 B．矩形 C．菱形 D．正方形
發布：2025/5/22 3:30:2組卷：456引用：3難度：0.5
解析
3．如圖，在矩形ABCD中，對角線AC，BD交于點O，要使該矩形成為正方形，則應添加的條件是（　　）
A．CD=AD B．OD=CD C．BD=AC D．∠AOB=60°
發布：2025/5/22 10:0:1組卷：238引用：3難度：0.7
解析

相關試卷

1．在平行四邊形ABCD的對角線AC與BD相交于點O，BC=5，AC=6，BD=8，則四邊形ABCD（ ）