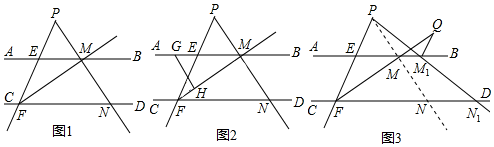
已知，如圖1，射線PE分別與直線AB、CD相交于E、F兩點(diǎn)，∠PFD的平分線與直線AB相交于點(diǎn)M，射線PM交CD于點(diǎn)N，設(shè)∠PFM=α，∠EMF=β，且60-2α+|β-30|=0．
（1）α=3030°，β=3030°；直線AB與CD的位置關(guān)系是AB∥CDAB∥CD；
（2）如圖2，若點(diǎn)G是射線MA上任意一點(diǎn)，且∠MGH=∠PNF，試找出∠FMN與∠GHF之間存在的數(shù)量關(guān)系，并證明你的結(jié)論；
（3）若將圖中的射線PM繞著端點(diǎn)P逆時(shí)針方向旋轉(zhuǎn)（如圖3），分別與AB、CD相交于點(diǎn)M1和點(diǎn)N1時(shí)，作∠PM1B的角平分線M1Q與射線FM相交于點(diǎn)Q，問在旋轉(zhuǎn)的過程中∠FPN1∠Q的值變不變？若不變，請(qǐng)求出其值；若變化，請(qǐng)說明理由．
60
-
2
α
∠
FP
N
1
∠
Q
【考點(diǎn)】平行線的判定與性質(zhì)．
【答案】30；30；AB∥CD
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/4 8:0:1組卷：1547引用：4難度：0.6
相似題
-
1．已知的三角形的三個(gè)內(nèi)角的度數(shù)和是180°，如圖是兩個(gè)三角板不同位置的擺放，其中∠ACB=∠CDE=90°，∠BAC=60°，∠DEC=45°．
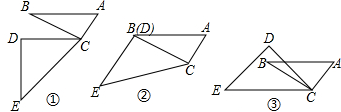
（1）當(dāng)AB∥DC時(shí)，如圖①，求∠DCB的度數(shù)．
（2）當(dāng)CD與CB重合時(shí)，如圖②，判斷DE與AC的位置關(guān)系，并說明理由．
（3）如圖③，當(dāng)∠DCB等于度時(shí)，AB∥EC．發(fā)布：2025/6/8 19:0:1組卷：172引用：4難度：0.5 -
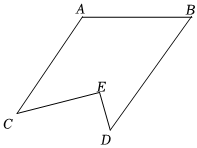2．如圖，AC，BD被AB所截，E為AB外一點(diǎn)，連接CE，ED，已知∠A=（90+x）°，∠B=（90-x）°，∠CED=90°，2∠C-∠D=α°．
（1）判斷AC與BD的位置關(guān)系，并說明理由；
（2）當(dāng)α=30°時(shí)，求∠C，∠D的度數(shù)；
（3）求∠C，∠D的度數(shù)（用含α的式子表示）．發(fā)布：2025/6/8 19:30:1組卷：83引用：2難度：0.7 -
3．將一副三角板按如圖放置，則下列結(jié)論：
①∠1=∠3；②如果∠2=30°，則有AC∥DE；③∠2+∠CAD=180°；④如果∠4=∠C，必有AB⊥ED．其中正確的有 （填寫序號(hào)）發(fā)布：2025/6/8 19:0:1組卷：354引用：6難度：0.7